Lesson 09: Matrix Algebra
Objective
- Learn the basic operations of the matrix algebra.
- Learn how to solve simultaneous equations by using MATLAB matrix operations.
Background
9.1 Matrix Operations and Functions
Transpose
Transpose
The transpose operator changes the rows of a matrix into columns and the columns into rows. In mathematics texts, you will often see the transpose indicated with superscript T (as in AT ). In MATLAB, the transpose operator is a single quote ('), so that the transpose of matrix A is A'.
| Syntax | Description |
|---|---|
| B = A' | Computes the complex conjugate transpose of A. |
| B = ctranspose(A) | This is an alternate way to execute A', but is rarely used. |
| B = A.' | Returns the non-conjugate transpose of A, that is, interchanges the row and column index for each element. |
| B = transpose(A) | This is an alternate way to execute A.' and enables operator overloading for classes. |
Complex Conjugate Transpose
The complex conjugate transpose of a matrix interchanges the row and column index for each element, reflecting the elements across the main diagonal. The operation also negates the imaginary part of any complex numbers.
For example, if B = A' and A(1,2) is 1+1i, then the element B(2,1) is 1-1i.
Complex Non-Conjugate Transpose
The non-conjugate transpose operator, A.', performs a transpose without conjugation. That is, it does not change the sign of the imaginary parts of the elements.
If A contains complex elements, then A.' does not affect the sign of the imaginary parts. For example, if A(3,2) is 1+2i and B = A.', then the element B(2,3) is also 1+2i.
Real Matrix
Create a 4-by-2 matrix, and find the conjugate transpose of A.
>> A = [2 1; 9 7; 2 8; 3 5];
>> B = A'
B = 2×4
2 9 2 3
1 7 8 5
The result is a 2-by-4 matrix. B has the same elements as A, but the row and column index for each element are interchanged. When no complex elements are present, A' produces the same result as A.'.
Create a matrix of real numbers and compute its transpose. B has the same elements as A, but the rows of B are the columns of A and the columns of B are the rows of A.
>> A = [1 2 3; 4 5 6; 7 8 9];
>> B = A.'
B =
1 4 7
2 5 8
3 6 9
Complex Matrix
Create a 2-by-2 matrix A with complex examples and find the conjugate transpose of A.
>> A = [0-1i 2+1i;4+2i 0-2i];
>> B = A'
A =
0.0000 + 1.0000i 4.000 - 2.000i
2.0000 - 1.0000i 0.000 + 2.000i
The result, B, contains the element of A with the row and column indices interchanged. The sign of the imaginary part of each number is also switched.
Create a matrix containing complex elements and compute its non-conjugate transpose. B contains the same elements as A, except the rows and columns are interchanged. The signs of the imaginary parts are unchanged.
>> A = [1 3 4-1i 2+2i; 0+1i 1-1i 5 6-1i];
>> B = A.'
B = 4×2 complex
1.0000 + 0.0000i 0.0000 + 1.0000i
3.0000 + 0.0000i 1.0000 - 1.0000i
4.0000 - 1.0000i 5.0000 + 0.0000i
2.0000 + 2.0000i 6.0000 - 1.0000i
Dot Product
Dot Product
The dot product (sometime called the scalar product) is the sum of the results you obtain when you multiply two vectors together, element by element.
| Syntax | Description |
|---|---|
| C = sum(A.*B) | To multiply two arrays, and then add the elements up to get the dot product. |
| C = dot(A,B) | Returns the scalar dot product of A and B. |
| C = dot(A,B,dim) | Evaluates the dot product of A and B along dimension, dim. The dim input is a positive integer scalar. |
- If A and B are vectors, then they must have the same length.
- If A and B are matrices or multidimensional arrays, then they must have the same size. In this case, the dot function treats A and B as collections of vectors. The function calculates the dot product of corresponding vectors along the first array dimension whose size does not equal 1.
Dimension to operate along, specified as a positive integer scalar. If no value is specified, the default is the first array dimension whose size does not equal 1.
Consider two 2-D input arrays, A and B:
- dot(A,B,1) treats the columns of A and B as vectors and returns the dot products of corresponding columns.
- dot(A,B,2) treats the rows of A and B as vectors and returns the dot products of corresponding rows.
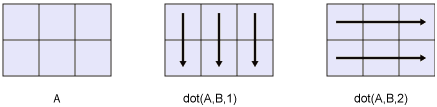
- dot returns conj(A).*B if dim is greater than ndims(A).
The scalar dot product of two real vectors of length n is equal to a mathematics text:
\[A\centerdot B=\sum\limits_{i=i}^{n}{{{A}_{i}}{{B}_{i}}={{A}_{1}}{{B}_{1}}+{{A}_{2}}{{B}_{2}}+\cdots +{{A}_{n}}{{B}_{n}}}\]
This relation is commutative for real vectors, such that dot(A,B) equals dot(B,A). If the dot product is equal to zero, then A and B are perpendicular.
For complex vectors, the dot product involves a complex conjugate. This ensures that the inner product of any vector with itself is real and positive definite.
\[U\centerdot V=\sum\limits_{i=1}^{n}{\overline{{{U}_{i}}} {{V}_{i}}}\]
Unlike the relation for real vectors, the complex relation is not commutative, so dot(U,V) equals conj(dot(V,U)).
Dot Product of Real Vectors
Create two simple, three-element vectors, then calculate the dot product of A and B.
>> A = [4 -1 2];
>> B = [2 -2 -1];
>> C = dot(A,B)
C = 8
The result is 8 since \(C = A(1) * B(1) + A(2) * B(2) + A(3) * B(3)\)
Dot Product of Complex Vectors
Create two complex vectors, and calculate the dot product of A and B.
>> A = [1+i 1-i -1+i -1-i];
>> B = [3-4i 6-2i 1+2i 4+3i];
>> C = dot(A,B)
C = 1.0000 - 5.0000i
The result is a complex scalar since A and B are complex. In general, the dot product of two complex vectors is also complex. An exception is when you take the dot product of a complex vector with itself.
Find the inner product of A with itself.
>> D = dot(A,A)
D = 8
The result is a real scalar. The inner product of a vector with itself is related to the Euclidean length of the vector, norm(A).
Dot Product of Matrices
Create two matrices, then find the dot product of A and B.
>> A = [1 2 3;4 5 6;7 8 9];
>> B = [9 8 7;6 5 4;3 2 1];
>> C = dot(A,B)
C = 1×3
54 57 54
The result, C, contains three separate dot products. dot treats the columns of A and B as vectors and calculates the dot product of corresponding columns. So, for example, C(1)=54 is the dot product of A(:,1) with B(:,1).
Find the dot product of A and B, treating the rows as vectors.
>> D = dot(A,B,2)
D = 3×1
46
73
46
In this case, D(1)=46 is the dot product of A(1,:) with B(1,:).
Matrix Multiplication
Matrix Multiplication
| Syntax | Description |
|---|---|
| C = A * B | C is the linear algebraic product of the matrices A and B. The number of columns of A must equal the number of rows of B. |
The matrix multiplication operator calculates the product of two matrices with the formula:
\[{{C}_{i,j}}=\sum\limits_{k=1}^{n}{{{A}_{i,k}}{{B}_{k,j}}}\]
Because matrix multiplication is a series of dot products, the number of columns in matrix A must equal the number of rows in matrix B. If matrix A is an m×n matrix, matrix B must be n×p, and the results will be × matrix.
For example: A is a 2×3 matrix and B is a 3×3 matrix. The result is a 2×3 matrix. In this example, we have

The two inner numbers must match, and the two outer numbers determine the size of the resulting matrix.
Matrix multiplication is not in general commutative, which means that \(A*B\ne B*A\). If both matrices are square, we can indeed calculate an answer for \(A*B\) and an answer for \(B*A\), but the answers are nor the same.
To see this, you can calculate the product of two matrices.
\(A=\left[ \begin{matrix}1 & 3 \\2 & 4 \\\end{matrix} \right]\), \(B=\left[ \begin{matrix}3 & 0 \\1 & 5 \\\end{matrix} \right]\)
>> A * B
ans =
6 15
10 20
>> B * A
ans =
3 9
11 23
The previous matrix product is not equal to the following element-wise product.
>> A .* B
ans =
3 0
2 20
Matrix Multiplication to Dot Product
Consider the following matrices:
\(A=\left[ \begin{matrix}1 & 2 & 3 \\\end{matrix} \right]\), \(B=\left[ \begin{matrix}3 \\4 \\5 \\\end{matrix} \right]\)
then
>> A*B
ans = 26
gives the same result as
>> dot(A,B)
ans = 26
Matrix multiplication results in an array in which each element is a dot product.
Matrix Power
Matrix Power
| Syntax | Description |
|---|---|
| C = A^B | Computes A to the B power and returns the result in C. |
| C = mpower(A,B) | This is an alternate way to execute A^B, but is rarely used. |
Raising a matrix to a power is equivalent to multiplying the matrix by itself the requisite number of times. For example, \({{A}^{2}}\) is the same as \(A*A\); \({{A}^{3}}\) is the same as \(A*A*A\).
Recalling that the number of columns in the first matrix of a multiplication must be equal to the number of rows in the second matrix, we see that in order to raise a matrix to a power, the matrix must be square (have the same number of rows and columns). Consider the matrix
\[A=\left[ \begin{matrix}\begin{matrix}1 & 2 & 3 \\\end{matrix} \\\begin{matrix}4 & 5 & 6 \\\end{matrix} \\\end{matrix} \right]\]
If we tried to square this matrix, we would get an error statement because of the rows and columns mismatch:
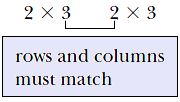
Square a Matrix
Create a 2-by-2 matrix and square it.
>> A = [1 2; 3 4];
>> C = A^2
C = 2×2
7 10
15 22
>> D = A * A
D = 2×2
7 10
15 22
The syntax A^2 is equivalent to A*A.
Matrix Inverse
Matrix Inverse
A matrix X is invertible if there exists a matrix Y of the same size such that \(XY=YX={{I}_{n}}\), where \({{I}_{n}}\) is the n×n identity matrix. The matrix Y is called the inverse of X.
A matrix that has no inverse is singular. A square matrix is singular only when its determinant is exactly zero.
| Syntax | Description |
|---|---|
| Y = X^(-1) | X^(-1) is equivalent to inv(X). |
| Y = inv(X) | Computes the inverse of square matrix X. |
Inverse Matrix
Compute the inverse of a 3-by-3 matrix.
>> X = [1 0 2; -1 5 0; 0 3 -9];
>> inv(X)
ans = 3×3
0.8824 -0.1176 0.1961
0.1765 0.1765 0.0392
0.0588 0.0588 -0.0980
>> X^-1
ans = 3×3
0.8824 -0.1176 0.1961
0.1765 0.1765 0.0392
0.0588 0.0588 -0.0980
We can show that multiplying the inverse of A by A gives the identity matrix: (\({{A}^{-1}}A=A{{A}^{-1}}=A\frac{1}{A}=1\))
>> inv(X)*X
ans = 3×3
1.0000 0.0000 0.0000
0.0000 1.0000 0.0000
0.0000 0.0000 1.0000
>> X*inv(X)
ans = 3×3
1.0000 0.0000 0.0000
0.0000 1.0000 0.0000
0.0000 0.0000 1.0000
Determinants
Determinants
| Syntax | Description |
|---|---|
| d = det(A) | Returns the determinant of square matrix A. |
Determinants are used in linear algebra and are related to the matrix inverse. If the determinant of a matrix is 0, the matrix does not have an inverse, and we say that it is singular. Determinants are calculated by multiplying together the elements along the matrix’s left-to-right diagonals and subtracting the product of the right-to-left diagonals. For example, for a 2×2 matrix:
\[A = \left[ {\begin{array}{*{20}{c}}{{A_{11}}}&{{A_{12}}}\\{{A_{21}}}&{{A_{22}}}\end{array}} \right]\]
the determinant is \(\left| A \right| = {A_{11}}{A_{22}} - {A_{12}}{A_{21}}\)
Thus, for \(A = \left[ {\begin{array}{*{20}{c}}1&2\\3&4\end{array}} \right]\)
\(\left| A \right| = (1)(4) - (2)(3) = - 2\)
For a 3×3 matrix, \(A = \left[ {\begin{array}{*{20}{c}}{{A_{11}}}&{{A_{12}}}&{{A_{13}}}\\{{A_{21}}}&{{A_{22}}}&{{A_{23}}}\\{{A_{31}}}&{{A_{32}}}&{{A_{33}}}\end{array}} \right]\)
- Multiply each left-to-right diagonal and add them up:
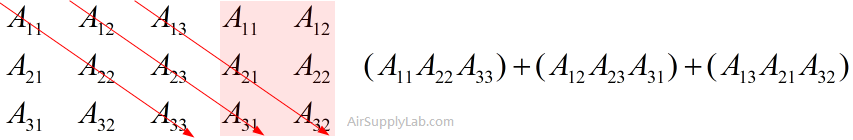
- Multiply each right-to-left diagonal and add them up.
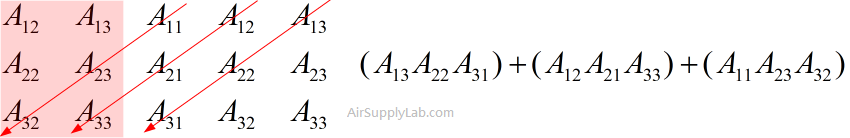
- Finally, subtract the second calculation from the first. For example, $A = \left[ {\begin{array}{*{20}{c}}
1&2&3\\
4&5&6\\
7&8&9
\end{array}} \right]$ , we might have
\[\begin{array}{l}
\left| A \right| = (1 \times 5 \times 9) + (2 \times 6 \times 7) + (3 \times 4 \times 8) - \left[ {(3 \times 5 \times 7) + (2 \times 4 \times 9) + (1 \times 6 \times 8)} \right]\\
= 225 - 225 = 0
\end{array}\]
Use MTLAB for the same calculation:
>> A = [1 2 3; 4 5 6; 7 8 9];
>> det(A)
ans = 0
The matrix with a determinant of zero do not have inverses. If you try to find the inverse of A, you will get a warning message:
>> inv(A)
Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 1.541976e-18.
ans =
1.0e+16 *
-0.4504 0.9007 -0.4504
0.9007 -1.8014 0.9007
-0.4504 0.9007 -0.4504
Calculate Determinant of Matrix
Create a 3-by-3 square matrix, A. Calculate the determinant of A and the inverse of A
>> A = [1 -2 4; -5 2 0; 1 0 3];
>> d = det(A)
d = -32
>> inv(A)
ans =
-0.1875 -0.1875 0.2500
-0.4688 0.0313 0.6250
0.0625 0.0625 0.2500
Determine if Matrix Is Singular
Cross Products
Cross Products
| Syntax | Description |
|---|---|
| C = cross(A,B) | Returns the cross product of A and B. |
| C = cross(A,B,dim) | Evaluates the cross product of arrays A and B along dimension, dim. The dim input is a positive integer scalar. |
- If A and B are vectors, then they must have a length of 3.
- If A and B are matrices or multidimensional arrays, then they must have the same size. In this case, the cross function treats A and B as collections of three-element vectors. The function calculates the cross product of corresponding vectors along the first array dimension whose size equals 3.
Dimension to operate along, specified as a positive integer scalar. The size of dimension dim must be 3. If no value is specified, the default is the first array dimension whose size equals 3.
Consider two 2-D input arrays, A and B:
- cross(A,B,1) treats the columns of A and B as vectors and returns the cross products of corresponding columns.
- cross(A,B,2) treats the rows of A and B as vectors and returns the cross products of corresponding rows.
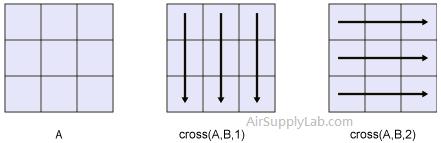
Cross returns an error if dim is greater than ndims(A).
Cross products are sometimes called vector products, because, unlike dot products, which return a scalar, the result of a cross product is a vector. The resulting vector is always at right angles (normal) to the plane defined by the two input vectors — a property that is called orthogonality.
We have two vectors in three-dimensional space that represent both a direction and a magnitude.
\(\vec i\), \(\vec j\) and \(\vec k\) are unit vectors in x, y, z directions.
\(\vec A \times \vec B = \left| {\matrix{ i & j & k \cr {{a_1}} & {{a_2}} & {{a_3}} \cr {{b_1}} & {{b_2}} & {{b_3}} \cr } } \right| = ({a_2}{b_3} - {a_3}{b_2})i - ({a_1}{b_3} - {a_3}{b_1})j + ({a_1}{b_2} - {a_2}{b_1})k\)
In MATLAB, the cross product is found using the function cross, which requires two inputs, the vectors A and B. Each of these MATLAB vectors must have three elements, since they represent the vector components in three-dimensional space.
Cross Product of Vectors
Create two 3-D vectors, A and B. Find the cross product of A and B. The result, C, is a vector that is perpendicular to both A and B.
>> A = [4 -2 1];
>> B = [1 -1 3];
>> C = cross(A,B)
C = -5 -11 -2
Use dot product to verify that C is perpendicular to A and B.
>> dot(C,A)==0 & dot(C,B)==0
ans = logical
1
Cross Product of Matrices
Create two 3×5 matrices, A and B.
Find the cross product of A and B.
>> C = cross(A,B)
C = 3×5
300 122 -114 -228 -181
-291 -198 -105 -30 55
87 136 101 234 175
The result, C, contains five independent cross products between the columns of A and B. For example, C(:,1) is equal to the cross product of A(:,1) with B(:,1).
9.2 Solutions of System of Linear Equations
Consider the following equations with three unknowns:
\[ 3x + 2y - z = 10\]
\[ - x + 3y + 2z = 5\]
\[ x - y - z = - 1\]
The equations can be rewritten by the matrices:
\[\underbrace {\left[ {\matrix{3 & 2 & -1 \cr { - 1} & 3 & 2 \cr 1 & { - 1} & { - 1} \cr} } \right]}_A\underbrace {\left[ {\matrix{x \cr y \cr z \cr} } \right]}_X = \underbrace {\left[ {\matrix{{10} \cr 5 \cr { - 1} \cr} } \right]}_B\quad \Rightarrow \quad AX = B\]
Solution Using the Matrix Inverse
Solution Using the Matrix Inverse
Probably the most straightforward way of solving this system of equations is to use the matrix inverse.
\(AX = B\quad \Rightarrow \quad X = {A^{ - 1}}B\)
As in all matrix mathematics, the order of multiplication is important. Since A is a 3×3 matrix, its inverse A-1 is also a 3×3 matrix. The multiplication A-1B :
![]()
works because the dimensions match up. The result is the 3×1 matrix X . If we change the order to BA-1 the dimensions would no longer match, and the operation would be impossible.
>> A = [3 2 -1; -1 3 2; 1 -1 -1];
>> B = [10; 5; -1];
>> X = inv(A)*B
X =
-2.0000
5.0000
-6.0000
>> X = A^-1*B
X =
-2.0000
5.0000
-6.0000
Solution Using Matrix Left Division
Solution Using Matrix Left Division
In MATLAB, we can use left division to solve the problem.
\[AX = B\quad \Rightarrow \quad X = {1 \over A}B\quad \Rightarrow X = A\backslash B\]
>> A = [3 2 -1; -1 3 2; 1 -1 -1];
>> B = [10; 5; -1];
>> X = A\B
X =
-2.0000
5.0000
-6.0000
Solution Using the Reverse Row Echelon Function
Solution Using the Reverse Row Echelon Function
| Syntax | Description |
|---|---|
| R = ref(A) | Return the reduced row echelon form of A using Gauss-Jordan elimination with partial pivoting. |
The linear equations can be solved by using the reduced row echelon function, rref. This function uses the Gauss-Jordan elimination technique.
>> A = [3 2 -1; -1 3 2; 1 -1 -1];
>> B = [10; 5; -1];
>> C = [A,B]
C =
3 2 -1 10
-1 3 2 5
1 -1 -1 -1
>> rref(C)
ans =
1 0 0 -2
0 1 0 5
0 0 1 -6
The solution to our problem is represented by the last column in the output array, and corresponds to the results achieved with the other methods.
9.3 Special Matrices
Ones and Zeros
Ones and Zeros
| Syntax | Description |
|---|---|
| X = ones | Returns the scalar 1. |
| X = ones(n) | Returns an n×n matrix of ones. |
| X = ones(sz1,…,szN) | Returns an sz1×...×szN array of ones where sz1,...,szN indicates the size of each dimension. For example, ones(2,3) returns a 2×3 array of ones. |
| X = ones(sz) | Returns an array of ones where the size vector, sz, defines size(X). For example, ones([2,3]) returns a 2×3 array of ones. |
Square Array of Ones
Create a 4×4 array of ones.
>> X = ones(4)
X = 4×4
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
3-D Array of Ones
Create a 2×3×2 array of ones.
>> X = ones(2,3,2)
X(:,:,1) =
1 1 1
1 1 1
X(:,:,2) =
1 1 1
1 1 1
| Syntax | Description |
|---|---|
| X = zeros | Returns the scalar 0. |
| X = zeros(n) | Returns an n×n matrix of zeros. |
| X = zeros(sz1,...,szN) | Returns an sz1×...×szN array of zeros where sz1,...,szN indicate the size of each dimension. For example, zeros(2,3) returns a 2×3 matrix. |
| X = zeros(sz) | Returns an array of zeros where size vector sz defines size(X). For example, zeros([2 3]) returns a 2×3 matrix. |
Matrix of Zeros
Create a 4×4 matrix of zeros.
>> X = zeros(4)
X = 4×4
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
3-D Array of Zeros
Create a 2×3×4 array of zeros.
>> X = zeros(2,3,4);
>> size(X)
ans = 1×3
2 3 4
Identity Matrix
Identity Matrix
| Syntax | Description |
|---|---|
| I = eye | Returns the scalar, 1. |
| I = eye(n) | Returns an n×n identity matrix with ones on the main diagonal and zeros elsewhere. |
| I = eye(n,m) | Returns an n×m matrix with ones on the main diagonal and zeros elsewhere. |
| I = eye(sz) | Returns an array with ones on the main diagonal and zeros elsewhere. The size vector, sz, defines size(I). For example, eye([2,3]) returns a 2×3 array with ones on the main diagonal and zeros elsewhere. |
Matrix multiplication is not in general commutative — \(AB \ne BA\)
However, for identity matrices, \(AI = IA\)
>> A = [1, 0, 2; -1, 4, -2; 5, 2, 1];
>> A*inv(A)
ans = 3×3
1 0 0
0 1 0
0 0 1
>> I = eye(3)
I = 3×3
1 0 0
0 1 0
0 0 1
>> A*I
ans = 3×3
1 0 2
-1 4 -2
5 2 1
>> I*A
ans = 3×3
1 0 2
-1 4 -2
5 2 1
Square Identity Matrix
Create a 4×4 identity matrix.
>> I = eye(4)
I = 4×4
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
Rectangular Matrix
Create a 2×3 identity matrix.
>> I = eye(2,3)
I = 2×3
1 0 0
0 1 0
Identity Vector
Create a 3×1 identity vector.
>> sz = [3,1];
>> I = eye(sz)
I = 3×1
1
0
0
Other Matrices
Other Matrices
| Syntax | Description |
|---|---|
| P = pascal(n) | Returns a Pascal’s Matrix of order n. P is a symmetric positive definite matrix with integer entries taken from Pascal's triangle. The inverse of P has integer entries. |
| M = magic(n) | Returns an n×n matrix constructed from the integers 1 through n2 with equal row and column sums. The order n must be a scalar greater than or equal to 3. |
| R = rosser | Returns the Rosser matrix in double precision. |
| gallery | The gallery contains over 50 different test matrices. The syntax for the gallery functions is different for each function, Use help to determine which is right for your needs. |
Matrix from Pascal's Triangle
Compute the fourth-order Pascal matrix.
>> A = pascal(4)
A = 4×4
1 1 1 1
1 2 3 4
1 3 6 10
1 4 10 20
Compute the lower triangular Cholesky factor of the third-order Pascal matrix, and verify it is involutory.
>> A = pascal(3,1)
A = 3×3
1 0 0
1 -1 0
1 -2 1
>> inv(A)
ans = 3×3
1 0 0
1 -1 0
1 -2 1
Third-Order Magic Square
Compute the third-order magic square M.
>> M = magic(3)
M = 3×3
8 1 6
3 5 7
4 9 2
The sum of the elements in each column and the sum of the elements in each row are the same.
>> sum(M)
ans = 1×3
15 15 15
>> sum(M,2)
ans = 3×1
15
15
15
Generate the Rosser matrix
>> rosser
ans = 8×8
611 196 -192 407 -8 -52 -49 29
196 899 113 -192 -71 -43 -8 -44
-192 113 899 196 61 49 8 52
407 -192 196 611 8 44 59 -23
-8 -71 61 8 411 -599 208 208
-52 -43 49 44 -599 411 208 208
-49 -8 8 59 208 208 99 -911
29 -44 52 -23 208 208 -911 99
Questions
Dot Product
- Compute the dot product of the following pairs of vectors, and then show that \(A \cdot B = B \cdot A\)
- \(A = \left[ {\begin{array}{*{20}{c}}1&3&5\end{array}} \right]\) \(B = \left[ {\begin{array}{*{20}{c}}{ - 3}&{ - 2}&4\end{array}} \right]\)
- \(A = \left[ {\begin{array}{*{20}{c}}0&{ - 1}&{ - 4}&{ - 8}\end{array}} \right]\) \(B = \left[ {\begin{array}{*{20}{c}}4&{ - 2}&{ - 3}&{24}\end{array}} \right]\)
- Use a dot product and the shopping list in the following Table to determine your total bill at the grocery store.
Item Number Needed Cost Milk 2 gallons \(\$ 3.50\) per gallon Eggs 1 dozen \(\$ 1.25\) per dozen Cereal 2 boxes \(\$ 4.25\) per box Soup 5 cans \(\$ 1.55\) per can Cookies 1 package \(\$ 3.15\) per package - Bomb calorimeters are used to determine the energy released during chemical reactions. The total heat capacity of a bomb calorimeter is defined as the sum of the products of the mass of each component and the specific heat capacity of each component, or
\[CP = \sum\limits_{i = 1}^n {{m_i}{C_i}} \]
where
\({{m_i}} = \)mass of component i, g
\({{C_i}} = \) heat capacity of component, i , J/(gK)
\(CP = \) total heat capacity, J/K
Find the total heat capacity of a bomb calorimeter, using the thermal data in the following Table.
Component Mass, g Heat Capacity, J?(gK) Steel 250 0.45 Water 100 4.2 Aluminum 10 0.90
Matrix Multiplication
- Compute the matrix product \(A*B\) of the following pairs of matrices:
- \(A = \left[ {\begin{array}{*{20}{c}}{12}&4\\3&{ - 5}\end{array}} \right]\) \(B = \left[ {\begin{array}{*{20}{c}}2&{12}\\0&0\end{array}} \right]\)
- \(A = \left[ {\begin{array}{*{20}{c}}1&3&5\\2&4&6\end{array}} \right]\) \(B = \left[ {\begin{array}{*{20}{c}}{ - 2}&4\\3&8\\{12}&{ - 2}\end{array}} \right]\)
Determinants and Inverses
- Recall that not all matrices have an inverse. A matrix is singular (i.e., it doesn't have an inverse) if its determinant equals 0 (i.e., \(\left| A \right| = 0\)). Use the determinant function to test whether each of the following matrices has an inverse:
\(A = \left[ {\begin{array}{*{20}{c}}2&{ - 1}\\2&5\end{array}} \right]\), \(B = \left[ {\begin{array}{*{20}{c}}4&2\\2&1\end{array}} \right]\), \(C = \left[ {\begin{array}{*{20}{c}}2&0&0\\1&2&2\\5&{ - 4}&0\end{array}} \right]\)
If an inverse exists, compute it.
Solving Linear Systems of Equations
- Solve the following system of equations, using both matrix left division and the inverse matrix method:
- \( - 2x + y = 3\)
\( x+y=10\) - \( 5x+3y-z=10\)
\( 3x+2y+z=4\)
\( 4x-y+3z=12\) - \( 3x+y+z+w=24\)
\( x-3y+7z+w=12\)
\( 2x+2y-3z+4w=17\)
\( x+y+z+w=0\)
- \( - 2x + y = 3\)