Lesson 08: Repetition Structures
Objective
- To learn how to write and use for loops.
- To learn how to write and use while loops.
Background
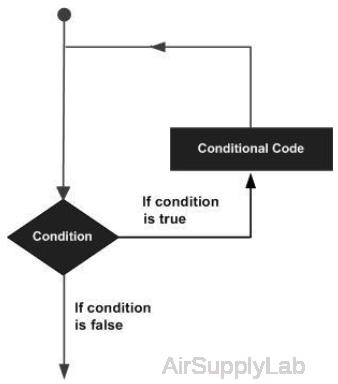
There may be a situation when you need to execute a block of code several times. In general, statements are executed sequentially. The first statement in a function is executed first, followed by the second, and so on. Programming languages provide various control structures that allow for more complicated execution paths. A loop statement allows us to execute a statement or group of statements multiple times. The drawing shows the general form of a loop statement for most programming languages. MATLAB provides various types of loops to handle looping requirements including: while loops, for loops,and nested loops. If you are trying to declare or write your own loops, you need to make sure that the loops are written as scripts and not directly in the Command Window. To start a new script, locate the button in the upper left corner of the window labeled New Script.
8.1 for and while Loops
for Loops
for loop to repeat specified number of times
| Syntax | Description |
|---|---|
| for index = valArray statements end |
Create a column vector, index, from subsequent columns of array valArray on each iteration. For example, index = valArray(:,1), the loop executes a maximum of n times, where n is the number of columns of valArray, given by numel(valArray(1,:)). The input valArray can be of any MATLAB data type, including a character vector, cell array, or struct. |
| for index=initVal:endVal statements end |
Increment the index variable from initVal to endVal by 1, and repeat execution of statements until index is greater than endVal. |
| for index=initVal:step:endVal ststements end |
Increment index by the value step on each iteration, or decrements index when step is negative. |
- The loop starts with a for statement and ends with the word end.
- The first line in the loop defines the number of times the loop will repeat, using an index matrix.
- The index of a for loop must be a variable.
- If the valArray is a row vector, the elements are used one at a time — once for each time through the loop.
- if the valArray is a two-dimensional matrix, each time through the loop, the index will contain the next column in tn matrix.
- Once a for loop is completed, the index variable retains the last value used.
- Avoid assigning a value to the index variable within the loop statements. The for statement overrides any changes made to index within the loop.
- To iterate over the values of a single column vector, first transpose it to create a row vector.
Assign Matrix Values
Create a Hibert matrix of order 10
s = 10;
H = zeros(s);
for c = 1:s
for r = 1:s
H(r,c) = 1 / (r+c-1);
end
end
Consider the following code:
for k = 1:5
a(k) = k^2
end
k
That loop defines a new matrix, a, one element at a time. The following output in the command window:
a = 1
a = 1 4
a = 1 4 9
a = 1 4 9 16
a = 1 4 9 16 25
k = 5
Index from a Matrix
valArray is a column vector
for k = [1,3,7]
k
fprintf("---\n");
end
This example code will return:
k = 1
---
k = 2
---
k = 3
---
valArray is a row vector
valArray = [1;3;7];
for k = valArray
k
fprintf("---\n");
end
The example will show:
k =
1
3
7
---
Decrement Values
Step by increments of -0.2, and display the values.
for v = 1.0:-0.2:0.0
disp(v)
end
1
0.8000
0.6000
0.4000
0.2000
0
Combine for-loop with if statement
In the list of test scores, find how many are above 90?
scores = [76, 45, 98, 97];
count = 0;
for k=1:length(scores)
if scores(k)>90
count = count + 1
end
end
disp (count)
Repeat Statements for Each Matrix Column
for k=[1, 2, 3; 1, 4, 9; 1, 8, 27]
a = k'
end
Returns
a = 1 1 1
a = 2 4 8
a = 3 9 27
while Loops
while loop to repeat when condition is true
| Syntax | Description |
|---|---|
| while expression statements end |
Evaluates an expression, and repeats the execution of a group of statements in a loop while the expression is true.
|
An expression can include relational operators (such as < or ==) and logical operators (such as &&, ||, or ~). Use the logical operators and and or to create compound expressions. MATLAB evaluates compound expressions from left to right, adhering to operator precedence rules.
Within the conditional expression of a while...end block, logical operators & and | behave as short-circuit operators. This behavior is the same as && and ||, respectively. Since && and || consistently short-circuit in conditional expressions and statements, it is good practice to use && and || instead of & and | within the expression.
For example,
x = 42;
while exist('myfunction.m','file') && (myfunction(x) >= pi)
disp('Expressions are true')
break
end
The first part of the expression evaluates to false. Therefore, MATLAB does not need to evaluate the second part of the expression, which would result in an undefined function error.
Repeat Statements Until Expression Is False
Use a while loop to calculate factorial(10).
n = 10;
f = n;
while n > 1
n = n - 1;
f = f * n;
end
disp(['n! = ' num2str(f)])
n! = 3628800
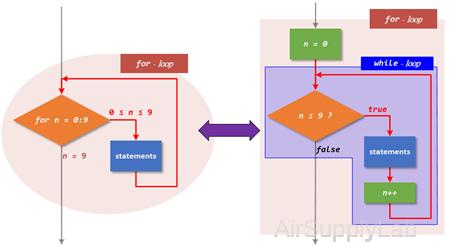
for - loop ↔ while - loop
Essentially every for loop can be written as a while loop.
This is a three step process:
- Notice that we need to initialize a loop variable (a while loop does not do this automatically). If our for loop began for x = 1:2:15, we must state that x = 1 initially, before our while loop begins.
- You must create a condition that is true while you want the loop to keep looping, and that becomes false when you want the loop to stop. Usually, this is the upper (or lower) bound on your loop variable. In our example, we'd want to keep looping while x is less than or equal to 15: x <= 15.
- Finally, before each iteration of our while loop ends, we must increment our loop variable. Notice that a for loop did that for us. Right before your end statement, you’ll likely place something like x = x+2 if you were converting the above example.
for - loop
for x = 1:2:15
disp(x)
end
while - loop
x = 1; % Step 1
while (x <= 15) % Step 2
disp(x)
x = x + 2; % Step 3
end
Practice Exercises 8.1
- Consider the following matrix of values:
$x = \left[ {45,{\rm{ }}23,{\rm{ }}17,{\rm{ }}34,{\rm{ }}85,{\rm{ }}33} \right]$
Use a for loop to find how many values are greater than 30? - Repeat Exercise 1, this time using the find function.
- Use a for loop to sum the elements of the matrix in Exercise 1.
- Use a while loop to find how many values are greater than 40 in Exercise 1?
- Use a while loop to create a vector containing the first 10 elements in the harmonic series, that is,
$1/1\quad 1/2\quad 1/3\quad 1/4\quad 1/5\quad \cdots \quad 1/10$
8.2 break and continue
break
break
Terminate execution of for or while loop.
| Syntax | Description |
|---|---|
| break | Terminates the execution of a for or while loop. Statements in the loop after the break statement do not execute. In nested loops, break exits only from the loop in which it occurs. Control passes to the statement that follows the end of that loop. |
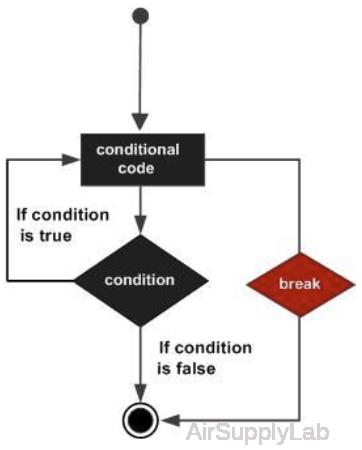
Note:
- The break statement exits a for or while loop completely. To skip the rest of the instructions in the loop and begin the next iteration, use a continue statement.
- break is not defined outside a for or while loop. To exit a function, use return.
Exit Loop Before Expression Is False
Sum a sequence of random numbers until the next random number is greater than an upper limit. Then, exit the loop using a break statement.
limit = 0.8;
s = 0;
while 1
tmp = rand;
if tmp > limit
break
end
s = s + tmp;
end
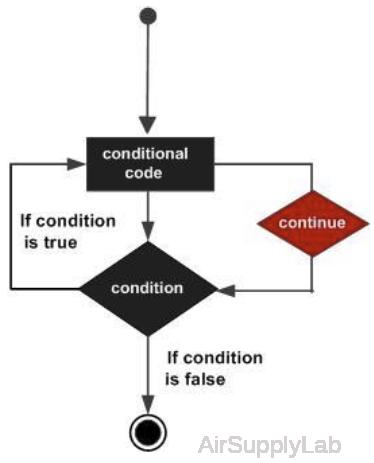
continue
continue
Pass control to next iteration of for or while loop.
| Syntax | Description |
|---|---|
| continue | Passes control to the next iteration of a for or while loop. It skips any remaining statements in the body of the loop for the current iteration. The program continues execution from the next iteration. continue applies only to the body of the loop where it is called. In nested loops, continue skips remaining statements only in the body of the loop in which it occurs. |
Note:
- The continue statement skips the rest of the instructions in a for or while loop and begins the next iteration. To exit the loop completely, use a break statement.
- continue is not defined outside a for or while loop. To exit a function, use return.
Selectively Display Values in Loop
Display the multiples of 7 from 1 through 50. If a number is not divisible by 7, use continue to skip the disp statement and pass control to the next iteration of the for loop.
for n = 1:50
if mod(n,7)
continue
end
disp(['Divisible by 7: ' num2str(n)])
end
Divisible by 7: 7
Divisible by 7: 14
Divisible by 7: 21
Divisible by 7: 28
Divisible by 7: 35
Divisible by 7: 42
Divisible by 7: 49
Skip to Next Loop Iteration
Count the number of lines of code in the file magic.m. Skip blank lines and comments using a continue statement. continue skips the remaining instructions in the while loop and begins the next iteration.
fid = fopen('magic.m','r');
count = 0;
while ~feof(fid)
line = fgetl(fid);
if isempty(line) || strncmp(line,'%',1) || ~ischar(line)
continue
end
count = count + 1;
end
count
fclose(fid)
count = 31
Nested Loops
You can place one or several loops inside another loop. Internal loops can be of the same or different types:
s = 0;
for i = 1:3
for j = 1:2
s = s + i + j;
end
end
fprintf("s = %d \n", s)
s = 21
s = 0;
for i = 1:3
j = 1;
while j <= 2
s = s + i + j;
j = j + 1;
end
end
fprintf("s = %d \n", s)
s = 21
Find the Maximum Value
Find the maximum value from matrix x.
$x = \left[ {\matrix{
1 & 2 & 6 & 3 \cr
4 & 8 & 2 & 1 \cr
{12} & {18} & 3 & 5 \cr
6 & 4 & 2 & {13} \cr
} } \right]$
If you use the max function
max(x)
MATLAB will return the maximum value in each column.
ans = 12 18 6 13
We can develop a program to find the maximum value.
[row, cols] = size(x);
maximum = x(1,1);
for k = 1:cols % External for loop ----------+
for j = 1:rows % Internal for loop ------+ |
if x(j,k) > maximum % if structure -------+ | |
maximum = x(i,j); % | | |
end % -------------------+ | |
end % -----------------------+ |
end % ---------------------------+
disp(['Maximum value is ' num2str(maximum)])
Maximum value is 18
Convert a Matrix into a Vector
Having two variables, one changing more quickly than the other, is extremely useful when working with matrices. Let's say we wanted to create a vector V from a matrix M without using the colon operator. We could take the following approach:
- Determine how many rows and columns are in the matrix using the size function.
- Create an empty vector V.
- Start on column 1 of the matrix. Loop through each row, adding that element onto the end of the vector.
- Then, move to column 2, 3, 4,... and repeat the process.
% Assume matrix M exists
[rows, cols] = size(M);
V = [];
for c = 1:cols
for w = 1:rows
V(end+1) = M(r, c);
end
end
disp(V)
Loops Structure vs. Vectorized code
In MATLAB, you'll often hear that it's bad to use loops when you could have instead used vector or matrix functions. This is because MATLAB’s built-in functions and arithmetic operations are optimized to use data stored as vectors or matrices in memory. Thus, whenever possible, use vectors, matrices, and their associated functions.
Timing Efficiency- Tic and Toc
MATLAB has two convenient commands that let you time how long an operation takes to compute. To start (and reset) a timer, use the command tic;. To stop the timer and display the amount of time elapsed, use toc;. If you’ve brainstormed a few different methods for solving a problem and want to have an idea of which method runs most quickly in MATLAB, use tic and toc !
We want to take the square root of any elements in a two-dimensional array whose value is greater than 5, and to square the remaining elements in the array.
$a = \left[ {\matrix{
1 & 2 & 3 \cr
6 & 4 & 9 \cr
5 & 8 & {27} \cr} } \right]$
To implement a code for this operation, we can use loops and branches:
clear; clc; close all;
a = [1 2 3; 6 4 9; 5 8 27];
tic
for ii = 1:size(a,1)
for jj = 1:size(a,2)
if a(ii,jj) > 5
a(ii,jj) = sqrt(a(ii,jj));
else
a(ii,jj) = a(ii,jj)^2;
end
end
end
toc
a
Elapsed time is 0.001692 seconds.
a =
1.0000 4.0000 9.0000
2.4495 16.0000 3.0000
25.0000 2.8284 5.1962
The vectorized code for this operation is:
clear; clc; close all;
a = [1 2 3; 6 4 9; 5 8 27];
tic
b = a > 5;
a(b) = sqrt(a(b));
a(~b) = a(~b) .^ 2;
toc
a
Elapsed time is 0.000823 seconds.
a =
1.0000 4.0000 9.0000
2.4495 16.0000 3.0000
25.0000 2.8284 5.1962
The vectorized code is significantly faster than the loops-and-branches version.
Practice Exercises 8.2
- Write the MATLAB code to calculate the value of the function
$f(t) = \left\{ {\matrix{
{\sin (t)} & {{\rm{: for}}\,{\rm{all }}\,t \,{\rm{ where }}\sin (t) > 0} \cr
0 & {{\rm{: elsewhere}}} \cr} } \right.$
for $ - 6\pi \le t \le 6\pi $ at intervals of ${\pi \over {10}}$.- Using loops to implement this function.
- Using vectorized code to implement it.
Questions
- Write the MATLAB statements required to calculate and print out the squares of all the even integers between 0 and 50. Create a table consisting of each integer and its square, with appropriate labels over each column.
- A store owner asks you to design a system for user in the checkout process. The system should:
- Prompt the user to enter the cost of the first item.
- Continue to prompt for additional items, until the user enters 0.
- Display the total.
- Prompt for the dollar amount the customer submits as payment.
- Display the charge due.
- A vectory is given by $X = \left[ {\matrix{-3.5 & -5 & 6.2 & 11 & 0 & 8.1 & -9 & 0 & 3 & -1 & 3 & 2.5 \cr} } \right]$. Using conditional statement and loops, develop a program that creates two vectors from X:
- Vector P contains all positive elements of X
- Vector N contains the negative elements of X.