Lab 05: Boolean Algebra and Verilog Simulation
Objective
Required Reading Materials
- Textbook: Digital Design: with an introduction to the Verilog HDL, 5th edition, Mano and Ciletti, ISBN-13: 978-0-13-277420-8
Chapter 2 - EE2440-FPGA Lab 02: Comparator, Decoders, and Encoders
Required Software
- ModelSim Starter Edition
Download ModelSim-Intel FPGA Edition (includes Starter Edition) from https://fpgasoftware.intel.com/20.1/?edition=lite
For the detailed installation for ModelSim, please check Exp#5.2.
Experiments
Every experiment section that requires you to build a circuit and test it has an asterisk (*). For those sections:
- For the in-class lab: Demonstrate the working circuit to your lab instructor.
- For online lab: Take a video to describe your circuit, upload the video to YouTube, and put the link in the report.
Exp #5.1 Boolean Algebra
Boolean Algebra is a mathematical approach to deriving equivalent functions. It is desirable to be able to simplify a function in order to design a circuit that uses fewer gates which can result in a more compact, lower-power design or to reduce the propagation delay of a signal through the circuit in order to speed up the circuit.
The table below shows the various identities that can be used to simplify a function.
Table 5.1.1: Boolean Algebra Identities
| Component/Device | Description | Quantity |
|---|---|---|
| Name | Identity | |
| Involution (Double Negative) | A = A | |
| Complementary Law | A + A = 1 | A • A = 0 |
| Idempotent Law | A + A = A | A • A = A |
| Null Law | A + 1 = 1 | A • 0 = 0 |
| Identity Law | A + 0 = A | A • 1 = A |
| Commutative Law | A + B = B + A | A B = B A |
| Associative Law | A + (B + C) = (A + B) + C | A (B C) = (A B) C |
| Distributive Law | A(B + C) = A B + A C | A + B C = (A + B)(A + C) |
| DeMorgan's Law | (A + B) = A B | (A B) = A + B |
| Law of Absorption | A + A B = A | A(A + B) = A |
| Consensus Theorem | AB + AC + BC = AB + AC | (A+B)(A+C)(B+C)=(A+B)(A+C) |
The easiest to derive a form of the function is the canonical representation, either Sum of Minterms or Product of Maxterms. A minterm is a product term that contains every input variable and a maxterm is a sum term that contains every input variable. Minterm i will evaluate to true (1) for input combination i. Maxterm i will evaluate to false (0) for input combination i. The table below shows the minterms (products) and maxterms (sums) for all possible input combinations for a 3-variable function with input variables A, B, and C.
Table 5.1.2: Minterm and Maxterm
| A | B | C | minterm | Maxterm |
|---|---|---|---|---|
| 0 | 0 | 0 | m0 = A B C | M0 = A + B + C |
| 0 | 0 | 1 | m1 = A B C | M1 = A + B + C |
| 0 | 1 | 0 | m2 = A B C | M2 = A + B + C |
| 0 | 1 | 1 | m3 = A B C | M3 = A + B + C |
| 1 | 0 | 0 | m4 = A B C | M4 = A + B + C |
| 1 | 0 | 1 | m5 = A B C | M5 = A + B + C |
| 1 | 1 | 0 | m6 = A B C | M6 = A + B + C |
| 1 | 1 | 1 | m7 = A B C | M7 = A + B + C |
A function can easily be expressed using a Sum of Minterms expression by taking the logical sum (OR) of the function's minterms (ANDs); i.e., for every input combination that produces a one at the output. Likewise, a function can easily be expressed using a Product of Maxterms expression by taking the logical product (AND) of the function's Maxterms (ORs); i.e., for every input combination that produces a zero at the output.
Consider the XOR and XNOR functions shown in this table.
Table 5.1.3: Truth Table of XOR and XNOR
| A | B | A ⊕ B | A ⊕ B |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
The exclusive-oR of A and B, A ⊕ B, can be expressed as the sum of minterms 1 and 2. That is,
A ⊕ B = m1 + m2 = Σm(1, 2) = A B + A B
The exclusive-nor of A and B, (A ⊕ B) can be expressed as the sum of minterms 0 and 3. That is,
(A ⊕ B) = m0 + m3 = Σm(0, 3) = A B + A B
The exclusive-or of A and B, A ⊕ B, can be expressed as the products of Maxterms 0 and 3. That is,
A ⊕ B = M0 • M3 = ΠM(0, 3) = (A + B)(A + B)
The exclusive-nor of A and B, (A ⊕ B) can be expressed as the product of Maxterms 1 and 2. That is,
(A ⊕ B) = M1 • M2 = ΠM(1, 2) = (A + B)(A + B)
Minterms and Maxterms
In general, the unique algebraic expression for any Boolean function can be obtained from its truth table by using an OR operator to combined all minterms for which the function is equal to 1.
Minterm
A minterm denoted as mi, where 0 ≦ i < 2n, is a product (AND) of the n variables in which each variable is complemented if the value assigned to it is 0 and uncomplemented if it is 1.
- 1-minterms = minterms for which the function F = 1.
- 0-minterms = minterms for which the function F = 0.
F = x y z + x y z + x y z + x y z
F = x y z + x y z + x y z + x y z
| x | y | z | minterms | Notation | F | F |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | x y z | m0 | 0 | 1 |
| 0 | 0 | 1 | x y z | m1 | 0 | 1 |
| 0 | 1 | 0 | x y z | m2 | 0 | 1 |
| 0 | 1 | 1 | x y z | m3 | 1 | 0 |
| 1 | 0 | 0 | x y z | m4 | 0 | 1 |
| 1 | 0 | 1 | x y z | m5 | 1 | 0 |
| 1 | 1 | 0 | x y z | m6 | 1 | 0 |
| 1 | 1 | 1 | x y z | m7 | 1 | 0 |
Any Boolean function can be expressed as a sum (OR) of its 1-minterms. The representation of the equation will be:
F(list of variables) = Σ(list of 1-minterm indices)
Ex. F = x y z + x y z + x y z + x y z = m3 + m5 + m6 + m7
or F(x,y,z) = Σ m(3,5,6,7)
The inverse of the function can be expressed as a sum (OR) of its 0-minterms. The representation of the equation will be:
F(list of variables) = Σ(list of 0-minterm indices).
Ex. F = x y z + x y z + x y z + x y z = m0 + m1 + m2 + m4
or F(x,y,z) = Σ m(0,1,2,4).
Maxterm
A maxterm denoted as Mi, where 0 ≦ i < 2n, is a sum (OR) of the n variables (literals) in which each variable is complemented if the value assigned to it is 1, and uncomplemented if it is 0.
- 1-maxterms = maxterms for which the function F = 1.
- 0-maxterms = maxterms for which the function F = 0.
F = (x+y+z)•(x+y+z)•(x+y+z)•(x+y+z)
F = (x+y+z)•(x+y+z)•(x+y+z)•(x+y+z)
| x | y | z | Maxterms | Notation | F | F |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | x+y+z | M0 | 0 | 1 |
| 0 | 0 | 1 | x+y+z | M1 | 0 | 1 |
| 0 | 1 | 0 | x+y+z | M2 | 0 | 1 |
| 0 | 1 | 1 | x+y+z | M3 | 1 | 0 |
| 1 | 0 | 0 | x+y+z | M4 | 0 | 1 |
| 1 | 0 | 1 | x+y+z | M5 | 1 | 0 |
| 1 | 1 | 0 | x+y+z | M6 | 1 | 0 |
| 1 | 1 | 1 | x+y+z | M7 | 1 | 0 |
Any Boolean function can be expressed as a product (AND) of its 0-maxterms. The representation of the equation will be:
F(list of variables) = Π(list of 0-maxterm indices)
Ex. F = (x + y + z)•(x + y + z)•(x + y + z)•(x + y + z) = M0•M1•M2•M4
or F(x,y,z) = Π M(0,1,2,4)
The inverse of the function can be expressed as a product (AND) of its 1-maxterms. The representation of the equation will be:
F(list of variables) = Π(list of 1-maxterm indices).
Ex. F =(x + y + z)•(x + y + z)•(x + y + z)•(x + y + z) = M3•M5•M6•M7
or F(x, y, z) = Π M(3,5,6,7).
Definition: Any Boolean function that is expressed as a sum of minterms or as a product of maxterms is said to be in its canonical form.
Examples: Minterms and Maxterms
Two Boolean functions: F = A + BC, and F = (A + BC). F and F are shown in the following truth table:
Table 5.1.4: Minterm and Maxterm
| A | B | C | minterm | Maxterm | F | F |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | m0 = A B C | M0 = A + B + C | 0 | 1 |
| 0 | 0 | 1 | m1 = A B C | M1 = A + B + C | 0 | 1 |
| 0 | 1 | 0 | m2 = A B C | M2 = A + B + C | 0 | 1 |
| 0 | 1 | 1 | m3 = A B C | M3 = A + B + C | 1 | 0 |
| 1 | 0 | 0 | m4 = A B C | M4 = A + B + C | 1 | 0 |
| 1 | 0 | 1 | m5 = A B C | M5 = A + B + C | 1 | 0 |
| 1 | 1 | 0 | m6 = A B C | M6 = A + B + C | 1 | 0 |
| 1 | 1 | 1 | m7 = A B C | M7 = A + B + C | 1 | 0 |
Sum of 1-Minterms
Express the Boolean function F = A + BC as a sum of minterms.
Solution 1:
| F = A + B C = A(B + B)(C + C) + (A + A)BC = A B C + A B C + A B C + A B C + A B C + A B C = m7 + m6 + m5 + m4 + m3 = Σ m(3,4,5,6,7) |
AND (multiply) has higher precedence than OR (add) expand 1st term by ANDing it with (B+B)(C+C), and 2nd term with (A+A). |
Solution 2:
Make a truth table for F = A + B C as shown in Table 5.1.4, to get the expression using the sum of minterms, we can calculate the sum of 1-minterms for function F:
F = m3 + m4 + m5 + m6 + m7 = Σ m(3,4,5,6,7) = A B C + A B C + A B C + A B C + A B C
Product of 0-Maxterms
Express the Boolean function F = A + BC as a product of maxterms.
Solution 1: First, we need to convert the function into product-of-OR terms by using the distributive law as follows:
| F = A + B C = (A + B)(A + C) = (A + B + C C)(A + B B + C) = (A + B + C)(A + B + C)(A + B + C)(A + B + C) = M0 • M1 • M2 = Π M(0,1,2) |
AND (multiply) has higher precedence than OR (add) use distributive law to change to product of OR terms expand 1st term by ORing it with (CC), and 2nd term with (BB). |
Solution 2:
Make a truth table for F = A + B C as shown in Table 5.1.4, to get the expression using the product of maxterms, we can calculate the product of 0-maxterms for function F:
F = M0 • M1 • M2 = Π M(0,1,2) = (A + B + C)(A + B + C)(A + B + C)
Sum of 0-Minterms
Express the Boolean function F = A + BC as a sum of minterms.
Solution 1:
| F = A + BC = A + (B • C) = A • (B + C) = (A • B)+(A • C) = (A B)(C + C) + A(B + B)C = A B C + A B C + A B C + A B C = m1 + m0 + m2 = Σ m(0,1,2) |
AND (multiply) has higher precedence than OR (add) use De Morgan's Law use distributive law to change to sum of AND terms expand 1st term by ANDing it with (C + C), and 2nd term with (B + B). |
Solution 2:
From the truth table as shown in Table 5.1.4, to get the expression using the sum of minterms, we can calculate the sum of 0-minterms for function F:
F = m0 + m1 + m2 = Σ m(0,1,2) = A B C + A B C + A B C
Product of 1-Maxterms
Express the Boolean function F = A + BC as a product of maxterms.
Solution 1:
|
F = A + BC = A + (B • C) |
AND (multiply) has higher precedence than OR (add) use De Morgan's Law use distributive law to change to product of OR terms expand 1st term by ORing it with (BB)and (CC), and 2nd term with (AA) |
Solution 2:
From the truth table as shown in Table 5.1.4, to get the expression using the sum of minterms, we can calculate the sum of 1-maxterms for function F:
F = M3 • M4 • M5 • M6 • M7 = Π M(3,4,5,6,7) = (A + B + C)(A + B + C)(A + B + C)(A + B + C)(A + B + C)
Question
- In this part of the experiment you should do the following (in your lab report):
- Explore three different functions for implementing the majority voter, V, described in Lab 4. The first, referred to as F1, is the function for V from Lab 4: F1 = AB + BC + AC.
- Write the truth table for the majority voter, V, with inputs A, B, and C (this was derived in Lab 4).
- Express V using the sum of minterms notation. Call this function F2.
- Express V using the product of maxterms notation. Call this function F3.
- Use the Boolean Algebra Identities (see Table 5.1) to prove that F1 = F2. Show the steps and label each step with the appropriate identity/Law.
Hint, you can use the Idempotent law to add additional redundant minterms. - Use the Boolean Algebra Identities to prove that F1 = F3. Show the steps and label each step with the appropriate identity/Law.
Exp #5.2 * Verilog HDL and Simulation
In this part of the experiment, you will verify the Consensus Theorem (A B + A C + B C = A B + A C) by implementing the following two functions using the Verilog Hardware Description Language (HDL), simulating the Verilog functions using the online simulator, and verifying that they both produce the same simulation waveform. (That F1 = F2 can also be verified by drawing a K-map for each.)
F1 = A B + A C + B C
F2 = A B + A C
The purpose of this experiment is to help you learn the basics of designing combinational logic circuits using a hardware description language (HDL), to learn the basics of how to model a circuit using gate-level modeling in Verilog, and how to verify that a circuit works properly using a simulator.
Follow along with the instructions provided to implement F1 and F2 in Verilog and simulate the circuits to verify that F1 is equivalent to F2. Record notes and observations in your manual to assist you in the future when designing circuits in Verilog.
ModelSim
Download ModelSim - Intel FPGA Edition (Includes Starter Edition) from https://fpgasoftware.intel.com/.
When you install ModelSim, the system will ask you to choose which edition you want to install. Since we do not need the license for this lab experiment, select ModelSim - IntelFPGA Starter Edition, and click Next >. Then, follow the setup instructions to install the ModelSim on your computer.
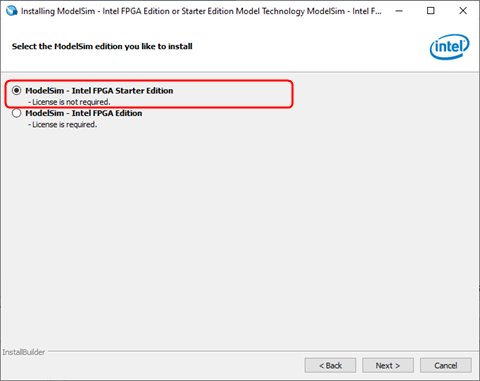
Figure 5.1: Install ModelSim-Intel FPGA Starter Edition, which License is not Required
After you install ModelSim, follow the steps to create a Verilog in ModelSim.
- Launch the
 ModelSim - Intel FPGA Starter Edition from the Windows Start button.
ModelSim - Intel FPGA Starter Edition from the Windows Start button. - Please read the verilog_lesson 12: Run Simulation on ModelSim (Pre-Simulation) and follow the instructions to learn how to create a project in ModelSim. Record your observations in your manual to assist you to create a new project for this assignment.
- On your Windows desktop, create a new folder for this lab experiment, and name it "EE2449_Lab05". Then, create a new project in ModelSim, and name it concensus.
- Add new Verilog files into the project
- concensus.v
- concensus_tb.v
Verilog File: concensus.v
The template below is for concensus.v. There is a module named concensus. The module has three input ports: A, B, and C; and two output ports F1 and F2.
/////////////////////////////////////////////////////////////////////////////// // Company: // Engineer: // // Create Data: 09:30:00 08/12/2020 // Design Name: // Module Name: concensus // Project Name: // Target Devices: // Tool versions: // Description: // // Dependencies: // // Revision: // Revision 0.01 - File Created // Additional Comments: // /////////////////////////////////////////////////////////////////////////////// module concensus( A, B, C, F1, F2); input A, B, C; output F1, F2; endmodule
Implement the functions F1 and F2 in the module concensus using Verilog HDL. The following logic primitives are available to be used:
not, and, or, nand, nor, xor, xnor
These primitives are the basic gates you tested in Lab 3. Notice that they are all in lower case (Verilog is case sensitive). When using a primitive, there is a set of parentheses ( ) after the primitive, and between the parentheses are the ports. The ports are the inputs and outputs to the function. The output port is always first because the basic logic functions (gates) only has one output. However, they can have multiple inputs. For example, we have seen both a two-input NAND and a three-input NAND. There is no need to indicate the number of inputs in Verilog, instead, all ports after the output port are assumed to be inputs).
Consider the Verilog statement: and (AB, A, B);
Notice that the output of the and primitive (gate) is given the name AB and that its inputs are A and B. Since the Verilog language is case sensitive, input A would be different from a. An input or output can have any name provided it consists only of letters, numbers, and underscores. Also, it can start only with a letter or underscore and it cannot be a reserved keyword like input or and, etc.
AB was the output name chosen here because it signifies the product term AB. Notice that the statement ends with a semicolon (;). Before proceeding, refer to the following Verilog file and convince yourself that the code actually implements the functions:
F1 = A B + B C + A C
F2 = A B + A C
Notice that the underscore (_) is often used to indicate "not"; e.g., A_ is A not or not A. Also, notice that the code for the design is indented (tabbed over) so that it is easy to see what is contained in the module. Extra white space is ignored by the HDL Compiler but you should use tab to make your code easier to read.
Type the following code for F1 and F2 into the concensus.v file. Also, modify the comments as shown and include you and your partner's (if you have one) names under Engineer as below:
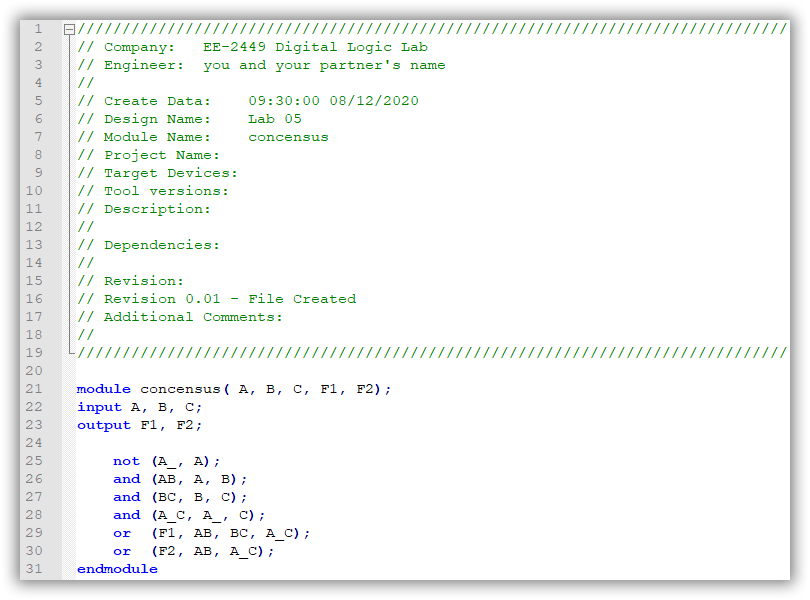
Figure 5.2: The Code for concensus.v File
After you finish entering the design, save the file.
Verilog File: concensus_tb.v
The following code is a template of a testbench provided for you with the inputs for the "UUT" (UUT means Unit-Under-Test; otherwise use "DUT" for Device-Under-Test); these are already inserted (ex: A, B, C). To test the circuits, values have to be loaded into the registers (components that hold values) A, B, and C. This is similar to what we have done in hardware on the breadboard where we have driven the inputs from the counter (which can hold values) or from the switches which can be mechanically/physically set to a particular value. The outputs will be driven on the wires F1 and F2. Under the comment Add stimulus here, you should assign various test input combinations to A, B, and C. Notice they have already been initialized to 0. In between each test case, insert a delay using statement #10 (the value of the delay does not matter in this case because we are only simulating the behavior and not the timing).
///////////////////////////////////////////////////////////////////////////////
// Company: EE-2449 Digital Logic Lab
// Engineer: you and your partner's name
//
// Create Data: 09:30:00 08/12/2020
// Design Name: Lab 05
// Module Name: concensus_tb
// Project Name:
// Target Devices:
// Tool versions:
// Description:
//
// Dependencies:
//
// Revision:
// Revision 0.01 - File Created
// Additional Comments:
//
///////////////////////////////////////////////////////////////////////////////
`timescale 1ns/1ns
module concensus_tb;
reg A, B, C; // Input
wire F1, F2; // Output
// Instantiate the Unit Under Test (UUT)
concensus UUT( .A(A), .B(B), .C(C), .F1(F1), .F2(F2));
initial begin
// Display the results
$monitor("time=%02d: ABC = %b%b%b F1 = %b, F2 = %b \n",$time, A, B, C, F1, F2 );
// Initialize Inputs
A = 0; B = 0; C = 0;
// Wait for 100 ns for the global reset to finish
#100;
// Add stimulus here
#20 $stop;
end
endmodule
The various test cases have been inserted into the code below. Note that this will test every combination from ABC = 000 to ABC = 111. The last statement sets the inputs back to 000 (similar to the counter rolling over). The last test case (ABC = 000) is redundant and was inserted so that you can easily see the test cases in the simulation waveform. Our test cases will start after a delay of 10 (indicated by #10). Note that one unit of delay has been set to 1 ns which is defined by the statement `timescale 1ns/1ns.
Type the following code to concensus_tb.v file, and save it.
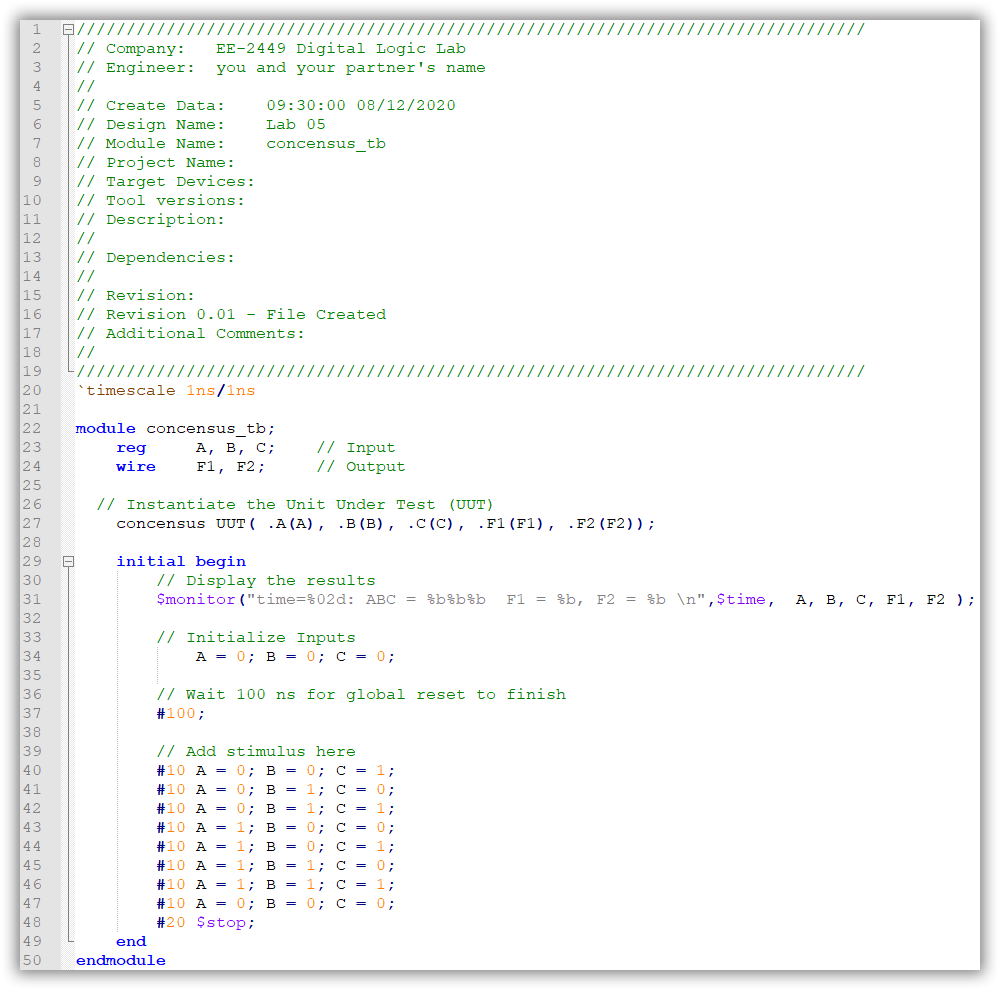
Figure 5.3: The Code for Testbench concensus_tb.v File
- Save the files and compile the code to ensure that there are no syntax errors, then run the simulation in ModelSim.
- Before running the testbench code, add A, B, C, F1, and F2 signals to the Wave window. Then click Simulate ➤ Run ➤ Run-All to execute the simulation.
- You should see the results in the Wave window as shown below:
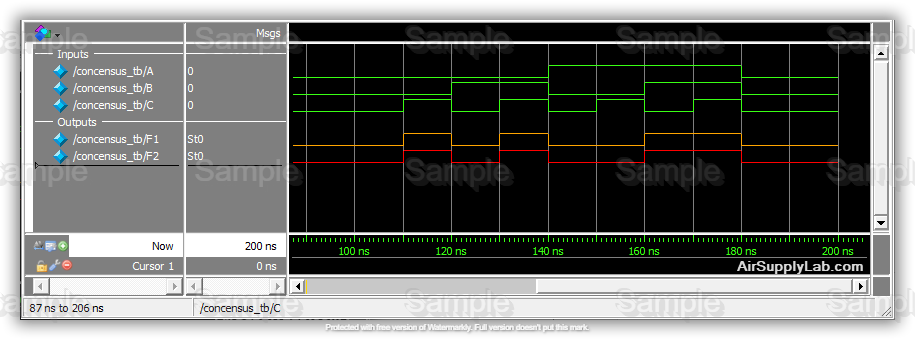
Figure 5.4: The Results in the Wave Window
In the waveform, note that starting at 100 ns, the values of ABC count from 000 to 111 and at 180 ns got back to 000. Reading the simulation waveform is similar to reading the oscilloscope waveforms except in this case we can see all inputs and outputs together. This is a very useful function and in fact, there are logical analyzers that are similar to oscilloscopes that capture and display multiple inputs and outputs in digital hardware design.
Note that F1 and F2 have the same waveform which proves that they are the same function. If you do not obtain the correct results, there must be an error in your design that you need to fix. In this example, if your results do not show that F1 and F2 are the same, there is an error in your design in the consensus module. Go back and fix it and repeat the steps to simulate the code.
Show your instructor your code and simulation results. Also, print out and paste the code and simulation results into your lab report.
Questions
- Describe intuitively why the term BC is redundant in F1.
Hint: Consider the other two terms AB and AC and the possible values of A. (Example: if A = 1, then F1 = BC + B. Is BC still needed?)
Exp #5.3 * Verilog HDL and Simulation II
Fill the boolean results for F1 = AB + BC + AC into the following truth table:
Table 5.3.1: Truth Table for F1 Boolean Expression
| A | B | C | F1 | minterm | Maxterm |
|---|---|---|---|---|---|
| 0 | 0 | 0 | m0 | M0 | |
| 0 | 0 | 1 | m1 | M1 | |
| 0 | 1 | 0 | m2 | M2 | |
| 0 | 1 | 1 | m3 | M3 | |
| 1 | 0 | 0 | m4 | M4 | |
| 1 | 0 | 1 | m5 | M5 | |
| 1 | 1 | 0 | m6 | M6 | |
| 1 | 1 | 1 | m7 | M7 |
Use ModelSim to implement the three functions for the majority voter in Verilog and run the simulation to verify that the three functions are the same.
F1 = AB + BC + AC
F2 = Sum of Minterms (determined in Exp #5.1 based on the Table 5.3.1)
F3 = Product of Maxterms (determined in Exp #5.1 based on the Table 5.3.1).
Follow the process outlined in Exp #5.2 to design your circuit in Verilog using gate-level modeling and to simulate your design. Show your instructor your code and simulation results. Also, print out and paste the code and simulation results into your lab report.
Questions
- What is the benefit of designing (and simulating) a circuit in a hardware description language (HDL) such as Verilog before building it in hardware?