Lesson 11: Symbolic Mathematics
Objective
- To learn how to create and manipulate symbolic variables, and use symbolic functions
- To learn how to solve symbolic expressions and equations
Background
10.1 Symbolic Data and Variables
Create Symbolic Variables, expressions, Functions, Matrices
Create Symbolic Variables, expressions, Functions, Matrices
| Syntax | Description |
|---|---|
| x = sym('x') | Creates symbolic variable x. |
| A = sym('a',[n1 ... nM]) | Creates an n1×...×nM symbolic array filled with automatically generated elements. For example, A = sym('a',[1 3]) creates the row vector A = [a1 a2 a3]. The generated elements a1, a2, and a3 do not appear in the MATLAB workspace. For multidimensional arrays, these elements have the prefix a followed by the element’s index using _ as a delimiter, such as a1_3_2. |
| A = sym('a',n) | creates an n×n symbolic matrix filled with automatically generated elements. |
| sym(___,set) | Creates a symbolic variable or array and sets the assumption that the variable or all array elements belong to a set. Here, set can be 'real', 'positive', 'integer', or 'rational'. You also can combine multiple assumptions by specifying a string array or cell array of character vectors. For example, assume a positive rational value by specifying set as ["positive" "rational"] or {'positive','rational'}. |
| sym(___,'clear') | Clears assumptions set on a symbolic variable or array. You can specify 'clear' after the input arguments in any of the previous syntaxes, except combining 'clear' and set. You cannot set and clear an assumption in the same function call to sym. |
| sym(num) | Converts a number or numeric matrix specified by num to a symbolic number or symbolic matrix. |
| sym(num,flag) | Uses the technique specified by flag for converting floating-point numbers to symbolic numbers. |
| sym(strnum) | Converts the character vector or string specified by strnum to an accurate symbolic number that avoid any approximation. |
| symexpr = sym(h) | Creates a symbolic expression or matrix symexpr from an anonymous MATLAB function associated with the function handle h. |
Create Symbolic Variables
Create the symbolic variables x and y.
x = sym('x')
x = x
y = sym('y')
y = y
Create Symbolic Vector
Create a 1×4 symbolic vector a with automatically generated elements a1, ..., a4.
a = sym('a',[1 4])
a = [ a1, a2, a3, a4]
Format the names of elements of a by using a format character vector as the first argument. sym replaces %d in the format character vector with the index of the element to generate the element names.
a = sym('x_%d',[1 4])
a = [ x_1, x_2, x_3, x_4]
This syntax does not create symbolic variables x_1, ..., x_4 in the MATLAB workspace. Access elements of a using standard indexing methods.
a(1)
a(2:3)
ans = x_1
ans = [ x_2, x_3]
Create Symbolic Matrix
Create a 3×4 symbolic matrix with automatically generated elements. The elements are of the form Ai_j, which generates the elements A1_1, ..., A3_4.
A = sym('A', [3 4])
A =
[ A1_1, A1_2, A1_3, A1_4]
[ A2_1, A2_2, A2_3, A2_4]
[ A3_1, A3_2, A3_3, A3_4]
Create a 4×4 matrix with the element names x_1_1, ..., x_4_4 by using a format character vector as the first argument. sym replaces %d in the format character vector with the index of the element to generate the element names.
B = sym('x_%d_%d',4)
B =
[ x_1_1, x_1_2, x_1_3, x_1_4]
[ x_2_1, x_2_2, x_2_3, x_2_4]
[ x_3_1, x_3_2, x_3_3, x_3_4]
[ x_4_1, x_4_2, x_4_3, x_4_4]
This syntax does not create symbolic variables A1_1, ..., A3_4, x_1_1, ..., x_4_4 in the MATLAB workspace. To access an element of a matrix, use parentheses.
A(2,3)
B(4,2)
ans = A2_3
ans = x_4_2
Create Symbolic Multidimensional Arrays
Create a 2×2×2 symbolic array with automatically generated elements a1,1,1,…,a2,2,2.
A = sym('a',[2 2 2])
A(:,:,1) =
[ a1_1_1, a1_2_1]
[ a2_1_1, a2_2_1]
A(:,:,2) =
[ a1_1_2, a1_2_2]
[ a2_1_2, a2_2_2]
Create Symbolic Numbers
Convert numeric values to symbolic numbers or expressions. Use sym on subexpressions instead of the entire expression for better accuracy. Using sym on entire expressions is inaccurate because MATLAB first converts the expression to a floating-point number, which loses accuracy. sym cannot always recover this lost accuracy.
inaccurate1 = sym(1/1234567)
inaccurate1 = \(\frac{{{\rm{7650239286923505}}}}{{{\rm{9444732965739290427392}}}}\)
accurate1 = 1/sym(1234567)
accurate1 = \(\frac{1}{{1234567}}\)
inaccurate2 = sym(sqrt(1234567))
inaccurate2 = \(\frac{{{\rm{4886716562018589}}}}{{{\rm{4398046511104}}}}\)
accurate2 = sqrt(sym(1234567))
accurate2 = \(\sqrt {1234567} \)
inaccurate3 = sym(exp(pi))
inaccurate3 = \(\frac{{{\rm{6513525919879993}}}}{{{\rm{281474976710656}}}}\)
accurate3 = exp(sym(pi))
accurate3 = \({e^\pi }\)
Create Large Symbolic Numbers
When creating symbolic numbers with 15 or more digits, use quotation marks to accurately represent the numbers.
inaccurateNum = sym(11111111111111111111)
inaccurateNum = 11111111111111110656
accurateNum = sym('11111111111111111111')
accurateNum = 11111111111111111111
When you use quotation marks to create symbolic complex numbers, specify the imaginary part of a number as 1i, 2i, and so on.
sym('1234567 + 1i')
ans = 1234567+i
Create Symbolic Expressions from Function Handles
Create a symbolic expression and a symbolic matrix from anonymous functions associated with MATLAB handles.
h_expr = @(x)(sin(x) + cos(x));
sym_expr = sym(h_expr)
sym_expr = cos(x)+sin(x)
h_matrix = @(x)(x*pascal(3));
sym_matrix = sym(h_matrix)
sym_matrix =
[ x, x, x]
[ x, 2*x, 3*x]
[ x, 3*x, 6*x]
Set Assumptions While Creating Variables
Create the symbolic variables x, y, z, and t while simultaneously assuming that x is real, y is positive, z rational, and t is positive integer.
x = sym('x','real');
y = sym('y','positive');
z = sym('z','rational');
t = sym('t',{'positive','integer'});
Check the assumptions on x, y, z, and t using assumptions.
assumptions
ans = [ in(x, 'real'), in(z, 'rational'), 1 <= t, 0 < y, in(t, 'integer')]
meaning: ans = \((x \in ℝ \quad z \in ℚ \quad 1 \le t\quad 0 < y\quad t \in ℤ )\)
For further computations, clear the assumptions using assume.
assume([x y z t],'clear')
assumptions
ans =
Empty sym: 1-by-0
Set Assumptions on Matrix Elements
Create a symbolic matrix and set assumptions on each element of that matrix.
A = sym('A%d%d',[2 2],'positive')
A = $\left( {\begin{array}{*{20}{c}}
{{A_{11}}}&{{A_{12}}}\\
{{A_{21}}}&{{A_{22}}}
\end{array}} \right)$
Solve an equation involving the first element of A. MATLAB assumes that this element is positive.
solve(A(1,1)^2-1, A(1,1))
ans = 1
Check the assumptions set on the elements of A by using assumptions.
assumptions(A)
ans = [ 0 < A11, 0 < A12, 0 < A21, 0 < A22]
Clear all previously set assumptions on elements of a symbolic matrix by using assume.
assume(A,'clear');
assumptions(A)
ans =
Empty sym: 1-by-0
Solve the same equation again.
solve(A(1,1)^2-1, A(1,1))
ans =
-1
1
Choose Conversion Technique for Floating-Point Values
Convert pi to a symbolic value.
Choose the conversion technique by specifying the optional second argument, which can be 'r', 'f', 'd', or 'e'. The default is 'r'. See the Input Arguments section for the details about conversion techniques.
r = sym(pi)
r = \(\pi \)
f = sym(pi,'f')
f = \(\frac{{{\rm{884279719003555}}}}{{{\rm{281474976710656}}}}\)
d = sym(pi,'d')
d = 3.1415926535897931159979634685442
e = sym(pi,'e')
e = \(\pi {\rm{ - }}\frac{{198 esp}}{{359}}\)
Create Symbolic Variables and Functions
Create Symbolic Variables and Functions
| Syntax | Description |
|---|---|
| syms var1 ... varN | Creates symbolic variables var1 ... varN. Separate different variables by spaces. syms clears all assumptions from the variables. |
| syms var1 ... varN [n1 ... nM] | Creates symbolic arrays var1 ... varN, where each array has the size n1×...×nM and contains automatically generated symbolic variables as its elements. For example, syms a [1 3] creates the symbolic array a = [a1 a2 a3] and the symbolic variables a1, a2, and a3 in the MATLAB workspace. For multidimensional arrays, these elements have the prefix a followed by the element’s index using _ as a delimiter, such as a1_3_2. |
| syms var1 ... varN n | Creates n×n symbolic matrices filled with automatically generated elements |
| syms ___ set | Sets the assumption that the created symbolic variables belong to set, and clears other assumptions. Here, set can be real, positive, integer, or rational. You also can combine multiple assumptions using spaces. For example, syms x positive rational creates a variable x with a positive rational value. |
| syms f(var1,...,varN) | Creates the symbolic function f and the symbolic variables var1,...,varN, which represent the input arguments of f. You can create multiple symbolic functions in one call. For example, syms f(x) g(t) creates two symbolic functions (f and g) and two symbolic variables (x and t). |
| syms f(var1,...,varN) [n1 ... nM] | Creates an n1×...×nM symbolic array with automatically generated symbolic functions as its elements. This syntax also generates the symbolic variables var1,...,varN that represent the input arguments of f. For example, syms f(x) [1 2] creates the symbolic array f(x) = [f1(x) f2(x)], the symbolic functions f1(x) and f2(x), and the symbolic variable x in the MATLAB workspace. For multidimensional arrays, these elements have the prefix f followed by the element’s index using _ as a delimiter, such as f1_3_2. |
| syms f(var1,...,varN) n | Creates an n×n symbolic matrix filled with automatically generated elements. |
| syms(symArray) | Creates the symbolic variables and functions contained in symArray, where symArray is either a vector of symbolic variables or a cell array of symbolic variables and functions. Use this syntax only when such an array is returned by another function, such as solve or symReadSSCVariables. |
| syms | Lists the names of all symbolic variables, functions, and arrays in the MATLAB workspace. |
| S = syms | Returns a cell array of the names of all symbolic variables, functions, and arrays. |
Create Symbolic Variables
Create symbolic variables x and y.
syms x y
Create a 1×4 symbolic vector a with the automatically generated elements a1, ..., a4.
syms a [1 4]
a
a = [ a1, a2, a3, a4]
Change the naming format of the generated elements by using a format character vector. Declare the symbolic variables by enclosing each variable name in single quotes. syms replaces %d in the format character vector with the index of the element to generate the element names.
syms 'a_%d' 'b_%d' [1 4]
a
b
a = [ a_1, a_2, a_3, a_4]
b = [ b_1, b_2, b_3, b_4]
Create Symbolic Equation
Create symbolic variables x and equation S.
syms x
S = x^2 - 2
Create Symbolic Functions
Create symbolic functions with one and two arguments.
syms s(t) f(x,y)
Both s and f are abstract symbolic functions. They do not have symbolic expressions assigned to them, so the bodies of these functions are s(t) and f(x,y), respectively.
Specify the following formula for f
f(x,y) = x + 2*y
Compute the function value at the point x = 1 and y = 2.
f(1,2)
ans = 5
Create Symbolic Functions with Matrices as Formulas
Create a symbolic function and specify its formula by using a symbolic matrix.
syms x
M = [x x^3; x^2 x^4];
f(x) = M
f(x) =
[ x, x^3]
[ x^2, x^4]
Compute the function value at the point x = 2:
f(2)
ans =
[ 2, 8]
[ 4, 16]
Compute the value of this function for x = [1 2 3; 4 5 6]. The result is a cell array of symbolic matrices.
xVal = [1 2 3; 4 5 6];
y = f(xVal)
y = 2×2 cell array
{2×3 sym} {2×3 sym}
{2×3 sym} {2×3 sym}
Access the contents of a cell in the cell array by using braces.
y{1}
ans =
[ 1, 2, 3]
[ 4, 5, 6]
List All Symbolic Variables, Functions, and Arrays
Create some symbolic variables, functions, and arrays.
syms a f(x)
syms A [2 2]
Display a list of all symbolic objects that currently exist in the MATLAB workspace by using syms.
syms
Your symbolic variables are:
A A1_1 A1_2 A2_1 A2_2 a f x
Instead of displaying a list, return a cell array of all symbolic objects by providing an output to syms.
S = syms
S = 8×1 cell array
{'A' }
{'A1_1'}
{'A1_2'}
{'A2_1'}
{'A2_2'}
{'a' }
{'f' }
{'x' }
Delete All Symbolic Variables, Functions, or Arrays
Create several symbolic objects.
syms a b c f(x)
Return all symbolic objects as a cell array by using the syms function. Use the clear function to delete all symbolic objects in the MATLAB workspace.
clear
Check that you deleted all symbolic objects by calling syms. The output is empty, meaning no symbolic objects exist in the MATLAB workspace.
syms
Reuse Names of Symbolic Objects
If you set a variable equal to a symbolic expression and then apply the syms command to the variable, MATLAB software removes the previously defined expression from the variable. For example,
syms a b
f = a + b
returns
f = a + b
If later you enter
syms f
f
then MATLAB removes the value a + b from the expression f:
f =
f
You can use the syms command to clear variables of definitions that you previously assigned to them in your MATLAB session. syms clears the assumptions of the variables: complex, real, integer, and positive. These assumptions are stored separately from the symbolic object. However, recreating a variable using sym does not clear its assumptions. For more information, see Delete Symbolic Objects and Their Assumptions.
Choose syms or sym Function
Choose syms or sym Function
In the Symbolic Math Toolbox, you can declare symbolic objects using either syms or sym. These two functions are conceptually different.
- The syms function creates a symbolic object that is automatically assigned to a MATLAB variable with the same name.
- The sym function refers to a symbolic object that can be assigned to a MATLAB variable with the same name or a different name.
Assign Symbolic Variables to MATLAB Variables
The syms function creates a variable dynamically. For example, the command syms x creates the symbolic variable x and automatically assigns it to a MATLAB variable with the same name.
syms x
x
x = x
The sym function refers to a symbolic variable, which you can then assign to a MATLAB variable with a different name. For example, the command f1 = sym('x') refers to the symbolic variable x and assigns it to the MATLAB variable f1.
f1 = sym('x')
f1 = x
Create Symbolic Number
Use the syms function to create a symbolic variable x and automatically assign it to a MATLAB variable x. When you assign a number to the MATLAB variable x, the number is represented in double-precision and this assignment overwrites the previous assignment to a symbolic variable. The class of x becomes double.
syms x
x = 1/33
x = 0.0303
class(x)
ans = 'double'
Use the sym function to refer to an exact symbolic number without floating-point approximation. You can then assign this number to the MATLAB variable x. The class of x is sym.
x = sym('1/33')
x = 1/33
class(x)
ans = 'sym'
Create Symbolic Variable with Assumptions
When you create a symbolic variable with an assumption, MATLAB stores the symbolic variable and its assumption separately.
Use syms to create a symbolic variable that is assigned to a MATLAB variable with the same name. You get a fresh symbolic variable with no assumptions. If you declare a variable using syms, existing assumptions are cleared.
syms x positive
syms x
assumptions
ans =
Empty sym: 1-by-0
Use sym to refer to an existing symbolic variable. If this symbolic variable was used in your MATLAB session before, then sym refers to it and its current assumption. If it was not used before, then sym creates it with no assumptions.
syms x positive
x = sym('x');
assumptions
ans = 0 < x
Create Many Symbolic Variables
To create many symbolic variables simultaneously, using the syms function is more convenient. You can create multiple variables in one line of code.
syms a b c
When you use sym, you have to declare MATLAB variables one by one and refer them to the corresponding symbolic variables.
a = sym('a');
b = sym('b');
c = sym('c');
Create Array of Symbolic Variables
To declare a symbolic array that contains symbolic variables as its elements, you can use either syms or sym.
The command syms a [1 3] creates a 1-by-3 symbolic array a and the symbolic variables a1, a2, and a3 in the workspace. The symbolic variables a1, a2, and a3 are automatically assigned to the symbolic array a.
clear all
syms a [1 3]
a
a =
[ a1, a2, a3]
whos
Name Size Bytes Class Attributes
a 1x3 8 sym
a1 1x1 8 sym
a2 1x1 8 sym
a3 1x1 8 sym
The command a = sym('a',[1 3]) refers to the symbolic variables a1, a2, and a3, which are assigned to the symbolic array a in the workspace. The elements a1, a2, and a3 are not created in the workspace.
clear all
a = sym('a',[1 3])
a =
[ a1, a2, a3]
whos
Name Size Bytes Class Attributes
a 1x3 8 sym
Symbolic Variable in Nested Function
To declare a symbolic variable within a nested function, use sym. For example, you can explicitly define a MATLAB variable x in the parent function workspace and refer x to a symbolic variable with the same name.
function primaryFx
x = sym('x')
function nestedFx
...
end
end
Nested functions make the workspace static, so you cannot dynamically add variables using syms.
10.2 Symbolic Algebra
Symbolic Expressions
Symbolic Expressions
Create Symbolic Expressions
Suppose you want to use a symbolic variable to represent the golden ratio
\(\phi = \frac{{1 + \sqrt 5 }}{2}\)
The command
phi = (1 + sqrt(sym(5)))/2;
achieves this goal. Now you can perform various mathematical operations on phi. For example,
f = phi^2 - phi - 1
f = (5^(1/2)/2 + 1/2)^2 - 5^(1/2)/2 - 3/2
Now suppose you want to study the quadratic function \(f = a{x^2} + bx + c\). First, create the symbolic variables a, b, c, and x:
syms a b c x
Then, assign the expression to f:
f = a*x^2 + b*x + c;
To create a symbolic number, use the sym command. Do not use the syms function to create a symbolic expression that is a constant. For example, to create the expression whose value is 5, enter f = sym(5). The command f = 5 does not define f as a symbolic expression.
Set Assumption Using Logical Operators
Combine these symbolic inequalities into a logical condition by using |.
syms x y
xy = x>=0 | y>=0;
Set the assumption represented by the condition using assume.
assume(xy)
Verify that the assumptions are set.
assumptions
ans =
0 <= x | 0 <= y
Evaluate Inequalities or Conditions
Define a range for a variable by combining two inequalities into a logical condition using &.
syms x
range = 0 < x & x < 1;
Return the condition at 1/2 and 10 by substituting for x using subs. The subs function does not evaluate the conditions automatically.
x1 = subs(range,x,1/2)
x2 = subs(range,x,10)
x1 =
0 < 1/2 & 1/2 < 1
x2 =
0 < 10 & 10 < 1
Evaluate the inequalities to logical 1 or 0 by using isAlways.
isAlways(x1)
isAlways(x2)
ans = logical
1
ans = logical
0
Symbolic Equations
Symbolic Equations
| Syntax | Description |
|---|---|
| A == B | Defines a symbolic equation. Use the equation as input to functions such as solve, assume, fcontour, and subs. |
| eq(A, B) | This is equivalent to A == B. |
Define and Solve Equation
Solve this trigonometric equation. Define the equation by using the == operator.
syms x
eqn = sin(x) == cos(x);
solve(eqn, x)
ans = pi/4
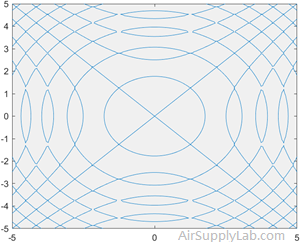
Plot Symbolic Equation
Plot the equation \(\sin ({x^2}) = \sin ({y^2})\) by using fimplicit. Define the equation by using the == operator.
syms x y
eqn = sin(x^2) == sin(y^2);
fimplicit(eqn)
Test Equality of Symbolic Expressions
Test the equality of two symbolic expressions by using isAlways.
syms x
eqn = x+1 == x+1;
isAlways(eqn)
ans = logical
1
eqn = sin(x)/cos(x) == tan(x);
isAlways(eqn)
ans = logical
1
Test Equality of Symbolic Matrices
Check the equality of two symbolic matrices by using isAlways.
A = sym(hilb(3));
B = sym([1 1/2 5; 1/2 2 1/4; 1/3 1/8 1/5]);
isAlways(A == B)
ans = 3×3 logical array
1 1 0
1 0 1
1 0 1
Compare a matrix and a scalar. The == operator expands the scalar into a matrix of the same dimensions as the input matrix.
A = sym(hilb(3));
B = sym(1/2);
isAlways(A == B)
ans = 3×3 logical array
0 1 0
1 0 0
0 0 0
10.2.1 Functions Used to Manipulate Expressions and Equations
Expand expressions and simplify
expand - Expand expressions and simplify inputs of functions by using identities
| Syntax | Description |
|---|---|
| expand(S) | Multiplies all parentheses in S, and simplifies inputs to functions such as cos(x + y) by applying standard identities. |
| expand(S,Name,Value) | Uses additional options specified by one or more name-value pair arguments. For example, specifying 'IgnoreAnalyticConstraints' as true uses convenient identities to simplify the input. |
Expand Symbolic Expression
syms x
p = (x - 2)*(x - 4);
expand(p)
ans = x^2 - 6*x + 8
Expand Trigonometric Expression
Expand the trigonometric expression cos(x + y). Simplify the cos function input x + y to x or y by applying standard identities.
syms x y
expand(cos(x + y))
ans = cos(x)*cos(y) - sin(x)*sin(y)
Expand Exponential Expression
Expand \({e^{{{(a + b)}^2}}}\). Simplify the exp function input, \({{{(a + b)}^2}}\), by applying standard identities.
syms a b
f = exp((a + b)^2);
expand(f)
ans = exp(a^2)*exp(b^2)*exp(2*a*b)
Expand Vector of Expressions
Expand expressions in a vector. Simplify the inputs to functions in the expressions by applying identities.
syms t
V = [sin(2*t), cos(2*t)];
expand(V)
ans = [ 2*cos(t)*sin(t), 2*cos(t)^2 - 1]
Expand Only Arithmetic and Suppress Expansion of Functions
By default, expand both expands terms raised to powers and expands functions by applying identities that simplify inputs to the functions. Expand only terms raised to powers and suppress expansion of functions by using 'ArithmeticOnly'.
Expand \({\left( {\sin (3x) - 1} \right)^2}\). By default, expand will expand the power ^2 and simplify the sin input 3*x to x.
syms x
f = (sin(3*x) - 1)^2;
expand(f)
ans = 2*sin(x) + sin(x)^2 - 8*cos(x)^2*sin(x) - 8*cos(x)^2*sin(x)^2 + 16*cos(x)^4*sin(x)^2 + 1
Suppress expansion of functions, such as sin(3*x), by setting ArithmeticOnly to true.
expand(f, 'ArithmeticOnly', true)
ans = sin(3*x)^2 - 2*sin(3*x) + 1
Simplify Log Input by Removing Constraints
Simplify the input of log function calls. By default, expand does not simplify logarithm input because the identities used are not valid for complex values of variables.
syms a b c
f = log((a*b/c)^2);
expand(f)
ans = log((a^2*b^2)/c^2)
Apply identities to simplify the input of logarithms by setting 'IgnoreAnalyticConstraints' to true.
expand(f,'IgnoreAnalyticConstraints',true)
ans = 2*log(a) + 2*log(b) - 2*log(c)
Factor Expressions
factor - Factors the expression or equation. The result is an array of the factors.
| Syntax | Description |
|---|---|
| F = factor(S) | Returns all irreducible factors of S in vector F. If S is an integer, factor returns the prime factorization of S. If S is a symbolic expression, factor returns the subexpressions that are factors of S. |
| F = factor(S, vars) | Returns an array of factors F, where vars specifies the variables of interest. All factors not containing a variable in vars are separated into the first entry F(1). The other entries are irreducible factors of S that contain one or more variables from vars. |
| F = factor(___,Name,Value) | Uses additional options specified by one or more Name, Value pair arguments. This syntax can use any of the input arguments from the previous syntaxes. |
Factor Integer Numbers
F = factor(823429252)
F = 2 2 59 283 12329
To factor integers greater than flintmax, convert the integer to a symbolic object using sym. Then place the number in quotation marks to represent it accurately.
F = factor(sym('82342925225632328'))
F = [ 2, 2, 2, 251, 401, 18311, 5584781]
To factor a negative integer, convert it to a symbolic object using sym.
F = factor(sym(-92465))
F = [ -1, 5, 18493]
Factor Symbolic Fractions
Factor the fraction 112/81 by converting it into a symbolic object using sym.
F = factor(sym(112/81))
F = [ 2, 2, 2, 2, 7, 1/3, 1/3, 1/3, 1/3]
Factor Polynomials
Factor the polynomial \({x^6} - 1 \).
syms x
F = factor(x^6-1)
F = [ x - 1, x + 1, x^2 + x + 1, x^2 - x + 1]
Factor the polynomial \({y^6} - {x^6}\).
syms y
F = factor(y^6-x^6)
F = [ -1, x - y, x + y, x^2 + x*y + y^2, x^2 - x*y + y^2]
Separate Factors Containing Specified Variables
Factor \({y^6} * {x^6}\) for factors containing x.
syms x y
F = factor(y^2*x^2,x)
F = [ y^2, x, x]
factor combines all factors without x into the first element. The remaining elements of F contain irreducible factors that contain x.
Factor the polynomial y for factors containing symbolic variables b and c.
syms a b c d
y = -a*b^5*c*d*(a^2 - 1)*(a*d - b*c);
F = factor(y,[b c])
F = [ -a*d*(a - 1)*(a + 1), b, b, b, b, b, c, a*d - b*c]
factor combines all factors without b or c into the first element of F. The remaining elements of F contain irreducible factors of y that contain either b or c.
Collect Coefficients
| Syntax | Description |
|---|---|
| collect(S) | Collects like terms |
Example:
clear all; clc
syms x
S = 2*(x+3)^2 + x^2 + 6*x + 9;
collect(S)
ans = 3*x^2 + 18*x + 27
Simplification Function
Simplification Function
| Syntax | Description |
|---|---|
| S = simplify(expr) | Performs algebraic simplification of expr. If expr is a symbolic vector or matrix, this function simplifies each element of expr. |
| S = simplify(expr,Name,Value) | Performs algebraic simplification of expr using additional options specified by one or more Name,Value pair arguments. |
Simplify Expressions
Simplify these symbolic expressions:
syms a
Z = a + 2*a + (a-3)^2 - (a^2 + 2*a +1)
simplify(Z)
Z = a + (a-3)^2 - a^2 - 1
ans = 8 - 5*a
syms x a b c
S1 = simplify(sin(x)^2 + cos(x)^2)
S2 = simplify(exp(c*log(sqrt(a+b))))
S1 = 1
S2 = (a + b)^(c/2)
Simplify Matrix Elements
Call simplify for this symbolic matrix. When the input argument is a vector or matrix, simplify tries to find a simpler form of each element of the vector or matrix.
syms x
M = [(x^2 + 5*x + 6)/(x + 2), sin(x)*sin(2*x) + cos(x)*cos(2*x);(exp(-x*i)*i)/2 - (exp(x*i)*i)/2, sqrt(16)];
S = simplify(M)
S =
[ x + 3, cos(x)]
[ sin(x), 4]
Extract numerator and denominator
| Syntax | Description |
|---|---|
| numden(S) | Finds the numerator of an express; this function is not valid for equations. |
| [N,D] = numden(S) | Finds both the numerator and the denominator of an expression; this function is not valid for equations. If S is a symbolic or a numeric matrix, then N is the symbolic matrix of numerators, and D is the symbolic matrix of denominators. Both N and D are matrices of the same size as S. |
Numerators and Denominators of Symbolic Numbers
Find the numerator and denominator of a symbolic number.
[n, d] = numden(sym(4/5))
n = 4
d = 5
Numerators and Denominators of Symbolic Expressions
Find the numerator and denominator of the symbolic expression.
syms x y
F1 = numden((x-5)/(x+5))
[n,d] = numden(x/y + y/x)
F1 = x - 5
n = x^2 + y^2
d = x*y
Numerators and Denominators of Matrix Elements
Find the numerator and denominator of each element of a symbolic matrix.
syms a b
[n,d] = numden([a/b, 1/b; 1/a, 1/(a*b)])
n =
[ a, 1]
[ 1, 1]
d =
[ b, b]
[ a, a*b]
10.3 Solving Expressions and Equations
| Syntax | Description |
|---|---|
| S = solve(eqn) | Solves an expression or equation with a single variable |
| S = solve(eqn,var) | Solves the equation eqn for the variable var. For example, solve(x + 1 == 2, x) solves the equation x + 1 = 2 for x. |
| S = solve(eqn,var,Name,Value) | Uses additional options specified by one or more Name,Value pair arguments. |
| Y = solve(eqns) | Solves a system equations and presents the solutions as a structure array |
| Y = solve(eqns,vars) | Solves the system of equations eqns for the variables vars and returns a structure that contains the solutions. |
| Y = solve(eqns,vars,Name,Value) | Uses additional options specified by one or more Name,Value pair arguments |
| [y1,...,yN] = solve(eqns,vars) | Solves the system of equations eqns for the variables vars. The solutions are assigned to the variables y1,...,yN. If you do not specify the variables, solve uses symvar to find the variables to solve for. In this case, the number of variables that symvar finds is equal to the number of output arguments N. |
| [y1,...,yN] = solve(eqns,vars,Name,Value) | Uses additional options specified by one or more Name,Value pair arguments. |
| [y1,...,yN,parameters,conditions] = solve(eqns,vars,'ReturnConditions',true) | Returns the additional arguments parameters and conditions that specify the parameters in the solution and the conditions on the solution. |
The Solve Function
Solve an Equation
When used with an expression, the solve function sets the expression equal to zero and solves for the roots.
syms x
E1 = x-3;
solve(E1)
ans = 3
Use the == operator to specify the equation sin(x) == 1 and solve it.
syms x
eqn = sin(x) == 1;
solx = solve(eqn,x)
solx = pi/2
Solve Quadratic Equation
Solve the quadratic equation without specifying a variable to solve for. solve chooses x to return the solution.
syms a b c x
eqn = a*x^2 + b*x + c == 0;
S = solve(eqn)
S =
-(b + (b^2 - 4*a*c)^(1/2))/(2*a)
-(b - (b^2 - 4*a*c)^(1/2))/(2*a)
Specify the variable to solve for and solve the quadratic equation for a.
Sa = solve(eqn,a)
Sa =
-(c + b*x)/x^2
Solve Expression with Multiple Variables
Solve the function for variable t.
syms P P0 r t
e3 = P==P0*exp(r*t);
solve(e3,t)
ans = log(P/P0)/r
Solve an Expression Set Equal to non-zero
To solve an expression set equal to something besides zero, you must use one of two approaches. If the equation is simple, you can transform it into an expression by subtracting the right-hand side from the left-hand side. For example,
\(5{x^2} + 6x + 3 = 10\)
could be reformulated as
\(5{x^2} + 6x - 7 = 0\)
syms x
E1 = 5*x^2 + 6*x - 7;
E2 = 5*x^2 + 6*x +3 == 10;
S1 = solve(E1)
S2 = solve(E2)
S1 =
- (2*11^(1/2))/5 - 3/5
(2*11^(1/2))/5 - 3/5
S2 =
- (2*11^(1/2))/5 - 3/5
(2*11^(1/2))/5 - 3/5
Notice that in both cases, the results are expressed as simply as possible, using fractions. You can use double function to convert a symbolic representation to a double-precision floating-point number:
double(s2)
ans =
-1.9266
0.7266
Solving Systems of Equations
Not only can the solve function solve single equations or expressions for any of the included variables, it can also solve systems of equations.
Solves Three Symbolic Equations
Solve the three embedded variables x , y , and z.
syms x y z
one = 3*x + 2*y -z == 10;
two = -x + 3*y + 2*z == 5;
three = x - y - z == -1;
List all three equations in the solve function:
answer = solve(one,two,three)
answer = struct with fields:
x: [1×1 sym]
y: [1×1 sym]
z: [1×1 sym]
To access the actual values, you’ll need to use the structure array syntax:
x=answer.x
y=answer.y
z=answer.z
x = -2
y = 5
z = -6
To force the results to be displayed without using a structure array and the associated syntax, we must assign names to the individual variables.
[X,Y,Z] = solve(one,two,three)
X = -2
Y = 5
Z = -6
10.4 Symbolic Plotting
Questions
- Create the following symbolic variables, using wither sym or syms command:
x, a, b, c
Use them to create thee following symbolic expressions or equations:
\(ex1 = {x^2} - 1\)
\(ex2 = {(x+1)^2}\)
\(ex3 = a{x^2}-1\)
\(eq1 = {x^2} == 1\)
\(eq2 = {(x+1)^2} = = 0\)
\(eq3 = a{x^2} == 1\)- Multiply ex1 by ex2, and name the result y1.
- Divide ex1 by ex2, and name the result y2.
- Use numden function to extract the numerator and denominator from y1 and y2.
- Use the factor, expand, collect, and simplify functions on y1, y2.
- Use the solve function to solve both ex1 and eq1.
- Use the solve function to solve ex3 and eq3 for both x and a.
- Consider the following system of linear equations:
\(5x + 6y - 3z = 10\)
\(3x - 3y + 2z = 14\)
\(2x - 4y - 12z = 24\)- Solve this system of equations by means of the linear algebra techniques discussed in Lab 09: Matrix Algebra.
- Define a symbolic equation representing each equation in the given system of equations. Use the solve function to solve for x , y , and z.
- Consider the following nonlinear system of equations:
\({x^2} + 5y - 3{z^2} = 15\)
\(4x + {y^2} - z = 10\)
\(x + y + z = 15\)
Solve the nonlinear system with the solve function. Use the double function on your results to simplify the answer.