Lesson 07: Arrays
An array is a way to group together several variables of a single data type. Arrays are useful primarily because the individual variables stored in an array can be accessed using an index number. This makes it easy to cycle through the array, accessing one variable after another.
Arrays are a fundamental data structure in C/C++. They allow you to store a collection of elements of the same data type in contiguous memory locations. However, arrays have an inherent limitation: all elements in an array must be of the same data type. This restriction can be quite restrictive when dealing with complex data structures that require multiple data types.
C/C++ offers a more versatile data structure called structures to overcome the limitations of arrays. Structures allow you to group variables of different data types together into a single unit. This provides greater flexibility in representing complex data relationships.
We will delve into structures in detail in Lesson 09: Structures, where you'll gain a thorough understanding of their structure, declaration, and usage. For now, keep in mind that structures serve as a powerful tool for managing and organizing data that cannot be accommodated by arrays.
7.1 Arrays
Arrays are a kind of data structure that can store a fixed-size sequential collection of elements of the same type. An array is used to store data collection, but it is often more useful to think of an array as a collection of variables of the same type.
Instead of declaring individual variables, such as number0, number1, ..., and number99, you declare one array variable, such as numbers, and use numbers[0], numbers[1], and ..., numbers[99] to represent individual variables. An index accesses a specific element in an array.
Defining an Array
Defining an Array
You may declare arrays of any data type, including classes. The general form of a singly dimensioned array is:
type variable [size];
type variable [size] = {initValue1, initValue2, … };
Where type specifies the data type of each element in the array, and size specifies the number of elements in the array.
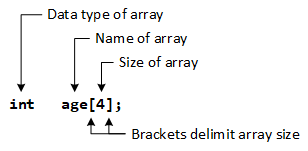
In C/C++, the name of an array always points to the first element of an array. Here, the address of the first element of an array is &age[0]. Also, age represents the address of the pointer where it is pointing. Hence, &age[0] is equivalent to age.
C arrays can be of any type. We define an array of ints, chars, doubles, etc. We can also define an array of pointers as follows. Here is the code to define an array of n char pointers or an array of strings.
char* A[n];
Specifying an Array Size
The array size must be a constant integer expression when declaring an array. The following declarations are some examples:
#define SIZE 4
int n = 4;
int m = 8;
float a0[SIZE]; // yes
float a1[4]; // yes
float a2[4*2 + 1]; // yes
float a3[sizeof(int) + 1]; // yes. sizeof() is considered an integer constant
float a4[-4]; // no, size must be > 0
float a5[0]; // no, size must be > 0
float a6[4.5]; // no, size must be an integer
float a7[(int)4.5]; // yes, typecast float to int constant
float a8[n]; // not allowed before C99
float a9[m]; // not allowed before C99
Array Elements
What are Array Elements?
An array is a collection of elements of the same data type stored in contiguous memory locations. Each element in an array has a unique index, which is a non-negative integer starting from 0. These elements are an array's building blocks and represent the data stored in the array structure.
Understanding Array Element Indexing
Indexing is a crucial aspect of accessing and manipulating array elements. Each element in an array is identified by its index, which serves as a pointer to its location in memory. The index of the first element is 0, the index of the second element is 1, and so on. This pattern continues until the last element, which has an index of n-1, where n is the size of the array.
Accessing Array Elements
Accessing an array element involves specifying its index within square brackets []. The index should be within the valid range of 0 to n-1, where n is the size of the array. For instance, to access the third element of an integer array named numbers, you would use:
int numbers[20]; // An integer array of 20 elements
int thirdElement = numbers[2]; // first element of array num
int lastElement = numbers[19]; // last (20th) element of array num
In this statement, the index 2 refers to the third element of the array, and the value of this element is assigned to the variable thirdElement.
Initializing Array Elements
Initializing Array Elements
Arrays can be initialized by using a bracketed list of initializers. For example,
int coins[6] = { 1, 5, 10, 25, 50, 100};
The first element is initialized to 1, the second to 5, etc.
The number of values between brackets ({}) can not be larger than the number of elements that we declare for the array between square brackets ([]).
You can also ignore the array size when you have a set of initialization values. The compiler will automatically calculate the size of the elements by counting the number of initial values.
int score[] = { 1, 5, 10, 25, 50, 100};
When setting the initial value of an array, if the number of set initial values is less than the number of elements of the array, the values of the rest of the elements will be directly filled with 0.
int num[5] = { 5, 10}; // num[] = {5, 10, 0, 0, 0}
Initializing Array to Zero
The array will be initialized to 0 in case we provide an empty initializer list or specify 0 in the initializer list.
int array[5] = {}; // initialize 5 ints to 0 -> array[5] = {0, 0, 0, 0, 0}
int array[5] = {0}; // initialize 5 ints to 0 -> array[5] = {0, 0, 0, 0, 0}
Designated Initializer (Supported by C++Builder)
This initializer is used to initialize a range of elements with the same value. (Not all compilers support this function)
int num[5] = {[1 ... 2] = 3}; // num[5] = {0, 3, 3, 0, 0}
int num[5] = {[0 ... 4] = 2}; // num[5] = {2, 2, 2, 2, 2}
You may also ignore the size of the array.
int num[] = {[1 ... 2] = 3}; // num[3] = {0, 3, 3}
int num[] = {[0 ... 4] = 2}; // num[5] = {2, 2, 2, 2, 2}
You can assign different index elements with different initial values as follows:
int x = 1233;
int a[10] = { [9] = x + 1, [2] = 3, [1] = 2, [0] = 1 };
Define a 10 elements array and initialize the last element to the value of x + 1 (or to 1234) and the first three elements to 1, 2, and 3, respectively.
Accessing Array Elements
Accessing Array Elements
All arrays consist of contiguous memory locations. The lowest address corresponds to the first element, and the highest address to the last element. All the elements can be accessed by indexing the array name. This is done by placing the element's index within square brackets ([]) after the array's name. For example, we declare an integer array score with 6 elements and initialization values as shown below:
int score[6] = { 69, 71, 88, 74, 60, 83};
The array variable score points to the address of the first elements of the array, which is the same as the address of the score[0].

Suppose the starting address of the score[0] is $1000. Then, the address of the score[1] will be $1004. Similarly, the address of the score[2] will be $1008, and so on. This is because the size of an int is 4 bytes.
Each element in the array can be accessed using an index number. But you cannot directly use an assignment operator (=) to assign one array to another. You have to set each individual element.
int arr1[5];
int arr2[5] = { 3, 6, 4, 5, 8};
arr1 = arr2; // Error, you can not assign one array to another one
arr1[0] = arr2[0]; // correct
arr1[1] = 57; // set the index number 1 of element (the 2nd element) to 57
arr2[2] = 78; // set the index number 2 of element (the 3rd element) to 78
sum = arr1[1] + arr2[2]; // add arr1[1] with arr2[2] together, then assign the result to the sum
float temp[8]; // declare a float array with 8 elements
7.2 Multidimensional Arrays
C/C++ programming language allows multidimensional arrays. The general form of declaring N-dimensional arrays:
type variable [size1][size2]… [sizeN];
Where type specifies the data type of each element in the array, and the size1, size2, …, sizeN are the sizes of each dimension.
Examples:
// Two-dimensional array
int twoD[10][20];
// Three dimensional array
int threeD[10][20][30];
Two Dimensional Arrays
The two-dimensional (2D) array is also known as a matrix. A matrix can be represented as a table of rows and columns.
type variable[rows][cols];
For example:
float x[2][4];
Here, we declared a two-dimensional array named x. The array can hold 8 elements. This array is the same as a table with 2 rows, and each row has 4 elements, as shown below:
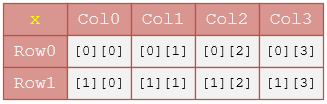
Initialization of a 2-D array
// Different ways to declare a 2D array with initialization values
int a[2][3] = { { 1, 3, 0},
{-1, 5, 9}};
int b[][3] = { { 1, 3, 0},
{-1, 5, 9}};
int c[2][3] = { 1, 3, 0, -1, 5, 9}};
Here, x is a two-dimensional array. The array can hold 6 elements.
Sum of Two Matrices
Sum of Two Matrices: C Code
// C program to find the sum of two matrices of order 2*2
#include <stdio.h>
int main()
{
float a[2][2], b[2][2], result[2][2];
int i, j;
// Taking input using nested for loop
printf("Enter elements of 1st matrix. \n");
for (i = 0; i < 2; ++i)
for (j = 0; j < 2; ++j) {
printf("Enter a[%d][%d]: ", i, j);
scanf("%f", &a[i][j]);
}
// Taking input using nested for loop
printf( "Enter elements of 2nd matrix. \n");
for (i = 0; i < 2; ++i)
for (j = 0; j < 2; ++j) {
printf( "Enter b[%d][%d]: ", i, j);
scanf("%f", &b[i][j]);
}
// adding corresponding elements of two arrays
for (i = 0; i < 2; ++i)
for (j = 0; j < 2; ++j) {
result[i][j] = a[i][j] + b[i][j];
}
// Displaying the sum
printf ("\nSum of Matrix: \n");
for ( i = 0; i < 2; ++i) {
for ( j = 0; j < 2; ++j)
printf("%8.2f", result[i][j]);
printf("\n");
}
return 0;
}Sum of Two Matrices: C++ Code
// C++ program to find the sum of two matrices of order 2*2
#include <iostream>
#include <iomanip>
using namespace std;
int main()
{
float a[2][2], b[2][2], result[2][2];
int i, j;
// Taking input using nested for loop
cout << "Enter elements of 1st matrix." << endl;
for (i = 0; i < 2; ++i)
for (j = 0; j < 2; ++j) {
cout << "Enter a["<< i << "][" << j << "]: ";
cin >> a[i][j];
}
// Taking input using nested for loop
cout << "Enter elements of 2nd matrix." << endl;
for (i = 0; i < 2; ++i)
for (j = 0; j < 2; ++j) {
cout << "Enter b[" << i << "][" << j <<"]: ";
cin >> b[i][j];
}
// adding corresponding elements of two arrays
for (i = 0; i < 2; ++i)
for (j = 0; j < 2; ++j) {
result[i][j] = a[i][j] + b[i][j];
}
// Displaying the sum
cout << endl;
cout << "Sum of Matrix: " << endl;
for ( i = 0; i < 2; ++i) {
for ( j = 0; j < 2; ++j)
cout << setw(8) << setprecision(2) << fixed << result[i][j];
cout << endl;
}
return 0;
}An example of an output:
Enter elements of 1st matrix.
Enter a[0][0]: 2
Enter a[0][1]: 0.5
Enter a[1][0]: -1.1
Enter a[1][1]: 2
Enter elements of 2nd matrix.
Enter b[0][0]: 0.2
Enter b[0][1]: 0
Enter b[1][0]: 0.23
Enter b[1][1]: 23
The sum of Matrix:
2.20 0.50
-0.87 25.00
Three Dimensional Arrays
The three-dimensional (3D) array is also known as a matrix. A matrix can be represented as a table of rows and columns.
type variable[page][rows][cols];
For example:
float x[2][3][4];
Here, we declared a three-dimensional array named x. The array can hold 24 elements. This array is the same as a table with two pages; each page has three rows, and each row has four elements, as shown below:
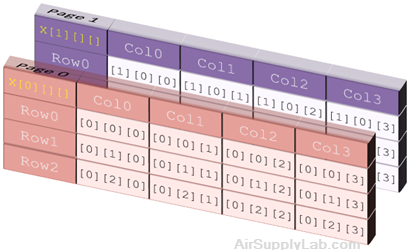
Initialization of a 3-D array
// Different ways to declare a 3D array with initialization values
int x[2][3][4] = {{{ 3, 4, 2, 3},
{ 0, -3, 9, 11},
{ 23, 12, 23, 2}},
{{ 13, 4, 56, 3},
{ 5, 5, 3, 5},
{ 3, 1, 4, 9}}};
int y[][3][4] = {{{ 3, 4, 2, 3},
{ 0, -3, 9, 11},
{ 23, 12, 23, 2}},
{{ 13, 4, 56, 3},
{ 5, 5, 3, 5},
{ 3, 1, 4, 9}}};
int z[2][3][4] = { 3, 4, 2, 3, 0, -3, 9, 11, 23, 12, 23, 2, 13, 4, 56, 3, 5, 5, 3, 5, 3, 1, 4, 9};
Create 3D Arrays
#include <stdio.h>
#include <iostream>
#include <iomanip>
using namespace std;
int main()
{
int x[2][3][4] = {{{ 3, 4, 2, 3},
{ 0, -3, 9, 11},
{ 23, 12, 23, 2}},
{{ 13, 4, 56, 3},
{ 5, 5, 3, 5},
{ 3, 1, 4, 9}}};
int y[][3][4] = {{{ 3, 4, 2, 3},
{ 0, -3, 9, 11},
{ 23, 12, 23, 2}},
{{ 13, 4, 56, 3},
{ 5, 5, 3, 5},
{ 3, 1, 4, 9}}};
int z[2][3][4] = { 3, 4, 2, 3, 0, -3, 9, 11, 23, 12, 23, 2, 13, 4, 56, 3, 5, 5, 3, 5, 3, 1, 4, 9};
int i, j, k;
cout << "x[][][]" << endl << endl;
for (i = 0; i < 2; i++) {
for (j = 0; j < 3; j++) {
for (k =0; k < 4; k++) {
cout << setw(4) << x[i][j][k];
}
cout << endl;
}
cout << endl;
}
cout << endl;
cout << "y[][][]" << endl << endl;
for (i = 0; i < 2; i++) {
for (j = 0; j < 3; j++) {
for (k =0; k < 4; k++) {
cout << setw(4) << y[i][j][k];
}
cout << endl;
}
cout << endl;
}
cout << endl;
cout << "z[][][]" << endl << endl;
for (i = 0; i < 2; i++) {
for (j = 0; j < 3; j++) {
for (k =0; k < 4; k++) {
cout << setw(4) << z[i][j][k];
}
cout << endl;
}
cout << endl;
}
cout << endl;
return 0;
}Multi-Dimensional Arrays
Declaration of a Multidimensional Array in C/C++:
type variable[size1][size2][size3] … [sizeN];
Where size1, size2, …, sizeN are the size of each dimension.
For example:
// Declare a 4-D array
int student[3][4][5][6];
// Declare a 5-D array
float score[5][6][5][6][5];
A 4-D array can be used to store a collection of data in Game design. For example, store 3D coordinates and 1D time into 4D arrays for each car in the game,[x][y][z][time]; then, we can use these arrays to check whether there is a collision that occurred between two vehicles or not.
7.3 Array Functions
Introduction to Array Functions
Array functions are a powerful tool in C/C++ that allows you to manipulate and process arrays in a concise and efficient manner. These functions provide a variety of operations, including searching, sorting, modifying, and transforming arrays. By utilizing array functions, you can enhance the readability and maintainability of your code while improving its overall performance.
Passing Arrays to Functions
Passing Arrays to Functions
In C/C++, arrays cannot be directly passed to functions as values. Instead, you pass the address of the first element of the array, which is essentially treated as a pointer to the array. This approach allows the function to access and modify the array elements.
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++) {
printf("%d ", arr[i]);
}
}
//------------------------------------------------------------------------------
int main() {
int numbers[] = {1, 2, 3, 4, 5};
int size = sizeof(numbers) / sizeof(numbers[0]);
printArray(numbers, size);
return 0;
}In this example, the printArray function takes an integer array arr and its size size as parameters. The function then iterates through the array and prints each element using the printf function.
Standard Library Array Functions (C++)
Standard Library Array Functions (C++)
The C++ Standard Library provides a rich collection of array functions that cater to various array operations. These functions are defined in the <algorithm> header file and offer a wide range of functionalities, including:
- std::copy: Copies elements from one array to another.
- std::fill: Fills an array with a specified value.
- std::find: Searches for an element in an array.
- std::count: Counts the occurrences of an element in an array.
- std::sort: Sorts an array in ascending or descending order.
- std::reverse: Reverses the order of elements in an array.
These functions greatly simplify array manipulation tasks and promote code reusability.
Finding the Sum of Array Elements
int sumArray(int arr[], int size) {
int sum = 0;
for (int i = 0; i < size; i++) {
sum += arr[i];
}
return sum;
}
//------------------------------------------------------------------------------
int main() {
int data[] = {10, 20, 30, 40, 50};
int size = sizeof(data) / sizeof(data[0]);
int totalSum = sumArray(data, size);
printf("The sum of the array elements is: %d", totalSum);
return 0;
}This example demonstrates the use of the sumArray function, which calculates the sum of all elements in an integer array. The function takes the array and its size as arguments and iterates through the array, accumulating the sum. Finally, it returns the total sum.
Sorting an Array
void sortArray(int arr[], int size) {
std::sort(arr, arr + size);
}
//------------------------------------------------------------------------------
int main() {
int numbers[] = {5, 2, 4, 1, 3};
int size = sizeof(numbers) / sizeof(numbers[0]);
sortArray(numbers, size);
printf("The sorted array is: ");
for (int i = 0; i < size; i++) {
printf("%d ", numbers[i]);
}
return 0;
}This example showcases using the std::sort function to sort an integer array in ascending order. The function takes the array and its size as arguments and applies the sorting algorithm directly to the array elements. The sorted array is then printed to the console.
Array functions are essential tools in C/C++ programming, enabling efficient and concise manipulation of arrays. The Standard Library provides a comprehensive collection of array functions, catering to various operations, simplifying array processing tasks, and enhancing code maintainability.
7.4 Matrix Operations
A matrix is a two-dimensional array often used for linear algebra.
Square Matrix is a matrix for which column and row numbers are the same (i.e., an n×n matrix).
Ebook: Further Mathematics for Science and Engineering.pdf
Matrix Addition
Matrix Addition — Both matrices should have the same size
Matrices of different sizes can not be added because the sum of two matrices is defined only when both have the same number of rows and columns.
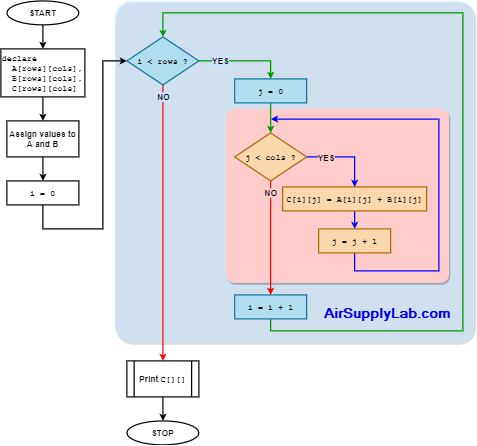
Algorithm to Add Two Matrices
for i = 0 to (rows - 1)
for j = 0 to (cols - 1)
C[i][j] = A[i][j] + B[i][j]Matrix Subtraction
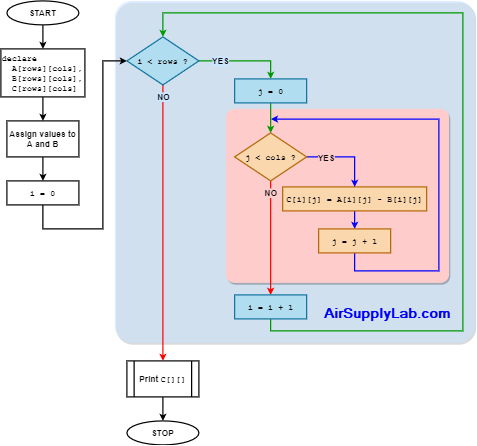
Matrix Subtraction — Both matrices should have the same size.
Matrices of different sizes cannot be subtracted because the subtraction of two matrices is defined only when both matrices have the same number of rows and the same number of columns.
Algorithm to Add Two Matrices
for i = 0 to (rows - 1)
for j = 0 to (cols - 1)
C[i][j] = A[i][j] - B[i][j]Matrix Multiplication
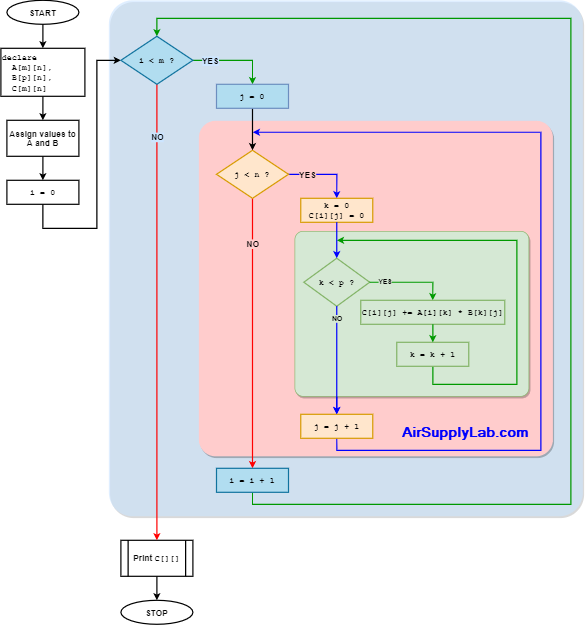
Matrix Multiplication
The product of two matrices is not defined when the number of columns in the first matrix and the number of rows in the second matrix are different.
${C_{m \times n}} = {A_{m \times p}} \times {B_{p \times n}} = \left[ {{C_{i,j}}} \right]$
$ \Rightarrow {C_{i,j}} = {a_{i,0}} \cdot {b_{0,j}} + {a_{i,1}} \cdot {b_{1,j}} + \cdots + {a_{i,k}} \cdot {b_{k,j}}$
$ \Rightarrow {C_{i,j}} = \left[ {\sum\limits_{k = 0}^{p-1} {{a_{i ,k }} \cdot {b_{k ,j}}} } \right]$
$C = A \times B = \left[ {\matrix{
{{a_{00}} \times {b_{00}} + {a_{01}} \times {b_{10}} + {a_{02}} \times {b_{20}}} & {{a_{00}} \times {b_{01}} + {a_{01}} \times {b_{11}} + {a_{02}} \times {b_{21}}} \cr
{{a_{10}} \times {b_{00}} + {a_{11}} \times {b_{10}} + {a_{12}} \times {b_{20}}} & {{a_{10}} \times {b_{01}} + {a_{11}} \times {b_{11}} + {a_{12}} \times {b_{21}}} \cr
} } \right]$
Algorithm to Multiply Two Matrices
for i = 0 to (m - 1)
for j = 0 to (n - 1)
for k = 0 to (p - 1)
C[i][j] += A[i][k] * B[k][j]Matrix Transpose
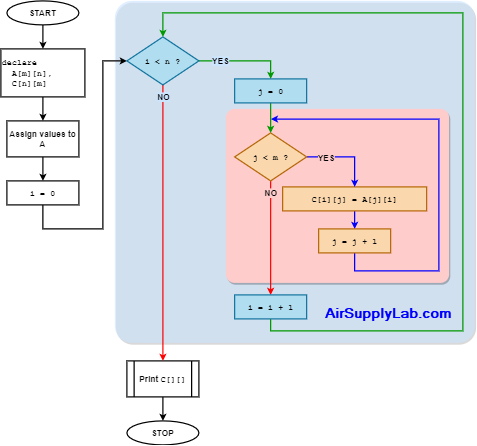
Matrix Transpose
Let A =[aij] be an m × n matrix. The transpose of A, denoted by AT, is the n × m matrix obtained by interchanging the rows and columns of A.
Algorithm for Matrix Transpose
for i = 0 to (n - 1)
for j = 0 to (m - 1)
C[i][j] = A[j][i]Determinant
The determinant of a matrix is the scalar value computed for a given square matrix. Linear algebra deals with the determinant computed using the elements of a square matrix. It can be considered the scaling factor for the transformation of a matrix. Useful in solving a system of linear equations, calculating the inverse of a matrix, and calculus operations.
The determinant of a matrix A,
$$\left[ {\matrix{
{{a_{00}}} & {{a_{01}}} & \cdots & {{a_{0(n - 1)}}} \cr
{{a_{10}}} & {{a_{11}}} & \ldots & {{a_{1(n - 1)}}} \cr
\vdots & \vdots & \ddots & \vdots \cr
{{a_{(n - 1)0}}} & {{a_{(n - 1)1}}} & \cdots & {{a_{(n - 1)(n - 1)}}} \cr
} } \right]$$
is commonly denoted $det(A)$.
If the $det(A)$ is 0, the matrix is singular, and if the $det(A)$ is 1, the matrix is unimodular.
A 2×2 determinant is defined to be: $\det \left( {\left[ {\matrix{{{a_{00}}} & {{a_{01}}} \cr{{a_{10}}} & {{a_{11}}} \cr} } \right]} \right) = {a_{00}} \times {a_{11}} - {a_{01}} \times {a_{10}}$
An n×n matrix determinant can be expanded to obtain:
$\eqalign{
& \left[ {\matrix{
{{a_{00}}} & {{a_{01}}} & \cdots & {{a_{0(n - 1)}}} \cr
{{a_{10}}} & {{a_{11}}} & \ldots & {{a_{1(n - 1)}}} \cr
\vdots & \vdots & \ddots & \vdots \cr
{{a_{(n - 1)0}}} & {{a_{(n - 1)1}}} & \cdots & {{a_{(n - 1)(n - 1)}}} \cr
} } \right] = {a_{00}} \times \left[ {\matrix{
{{a_{11}}} & {{a_{12}}} & \cdots & {{a_{1(n - 1)}}} \cr
\vdots & \vdots & \ddots & \vdots \cr
{{a_{(n - 1)1}}} & {{a_{(n - 1)2}}} & \cdots & {{a_{(n - 1)(n - 1)}}} \cr
} } \right] - {a_{01}} \times \left[ {\matrix{
{{a_{10}}} & {{a_{12}}} & \cdots & {{a_{1(n - 1)}}} \cr
\vdots & \vdots & \ddots & \vdots \cr
{{a_{(n - 1)0}}} & {{a_{(n - 1)2}}} & \cdots & {{a_{(n - 1)(n - 1)}}} \cr
} } \right] \cr
& + \cdots \pm {a_{0(n - 1)}} \times \left[ {\matrix{
{{a_{10}}} & {{a_{11}}} & \cdots & {{a_{1(n - 2)}}} \cr
\vdots & \vdots & \ddots & \vdots \cr
{{a_{(n - 1)0}}} & {{a_{(n - 1)1}}} & \cdots & {{a_{(n - 1)(n - 2)}}} \cr
} } \right] \cr} $
A general determinant for a matrix A has a value:
$\det (A) = \left| A \right| = \mathop \sum \limits_{i = 0}^n {a_{ij}}\,{C_{ij}} = \mathop \sum \limits_{i = 0}^n {a_{ij}}\, \cdot {( - 1)^{i + j}}{M_{ij}}$
Determinant of 2 x 2 Matrix
Determinant of 3 x 3 Matrix
& A = \left[ {\matrix{
a & b & c \cr
d & e & f \cr
g & h & i \cr
} } \right] \cr
& \left| A \right| = a\left[ {\matrix{
e & f \cr
h & i \cr
} } \right] - b\left[ {\matrix{
d & f \cr
g & i \cr
} } \right] + c\left[ {\matrix{
d & e \cr
g & h \cr
} } \right] \cr
& = a(e\,i - f\,h) - b(d\,i - f\,g) + c(d\,h - e\,g) \cr} $
C Program to Find Determinant of a Matrix
The following is an example of a C program that finds the determinant of a 4x4 matrix:
// C program to find Determinant of a matrix
#include <stdio.h>
#define N 4 // Dimension of input square matrix
// Function to get cofactor of mat[p][q]
// in temp[][]. n is current dimension of mat[][]
void getCofactor(int mat[N][N], int temp[N][N], int p, int q, int n)
{
int i = 0, j = 0;
// Looping for each element of the matrix
for (int row = 0; row < n; row++) {
for (int col = 0; col < n; col++) {
// Copying into temporary matrix only those element which are not in given row and column
if (row != p && col != q) {
temp[i][j++] = mat[row][col];
// Row is filled, so increase row index and reset col index
if (j == n - 1) {
j = 0;
i++;
}
}
}
}
}
//------------------------------------------------------------------------------
// Recursive function for finding the determinant of matrix.
// n is current dimension of mat[][].
int determinantOfMatrix(int mat[N][N], int n)
{
// Initialize result
int D = 0;
// Base case : if matrix contains single element
if (n == 1)
return mat[0][0];
// To store cofactors
int temp[N][N];
// To store sign multiplier
int sign = 1;
// Iterate for each element of first row
for (int f = 0; f < n; f++) {
// Getting Cofactor of mat[0][f]
getCofactor(mat, temp, 0, f, n);
D += sign * mat[0][f] * determinantOfMatrix(temp, n - 1);
// Terms are to be added with alternate sign
sign = -sign;
}
return D;
}
//------------------------------------------------------------------------------
// Function for displaying the matrix
void display(int mat[N][N], int row, int col)
{
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++)
printf(" %d", mat[i][j]);
printf("\n");
}
}
//------------------------------------------------------------------------------
// Driver code
int main()
{
int mat[N][N] = {{ 1, 0, 2, -1},
{ 3, 0, 0, 5},
{ 2, 1, 4, -3},
{ 1, 0, 5, 0}};
display(mat, N, N);
// Function call
printf("The determinant of the matrix is: %d",
determinantOfMatrix(mat, N));
return 0;
}Output:
1 0 2 -1 3 0 0 5 2 1 4 -3 1 0 5 0 The determinant of the matrix is: 30
Matrix Inverse
The inverse of a square matrix A, is called an invertible matrix. We write A-1 instead of ${1 \over A}$ because we do not divide by a matrix!
The inverse of a square matrix is another square matrix that produces the identity matrix when multiplied by the original matrix. The identity matrix is a square matrix with ones on the diagonal and zeros everywhere else.
You can obtain an inverse of a matrix using the following method:
- Calculate determinant of matrix, $det(A) = {\left| A \right|}$.
If ( $ {\left| A \right|} \ne 0$ ), then we can say the matrix A has an inverse. - Calculate the adjoint of the given matrix, $adj(A)$.
Adjoint can be obtained by taking the transpose of the cofactor matrix of the given square matrix. - Finally, the inverse of the matrix is given below: ${A^{ - 1}} = {{adj(A)} \over {\left| A \right|}}$
Matrix Division
Matrix division is an undefined function. To divide one matrix by another, the closed equivalent is multiplying by the inverse of the divisor matrix.
$$A/B = A \times {B^{ - 1}}$$
7.4 FIFO and FILO Buffers
What are FIFO and FILO Buffers?
FIFO and FILO are acronyms for two common data structures used in computer programming:
- FIFO (First-In, First-Out): A FIFO buffer operates like a queue, where the first added element is the first to be removed. This is analogous to a waiting line, where the first person in line is the first to be served.
- FILO (First-In, Last-Out): A FILO buffer operates like a stack, where the last added element is the first to be removed. This is similar to a stack of plates, where the plate you placed on top is the first one you can remove.
Both FIFO and FILO buffers are commonly used in various applications, such as data communication, data processing, and operating systems.
Implementing FIFO and FILO Buffers using Arrays
Arrays provide a convenient way to implement both FIFO and FILO buffers in C/C++. Here's a simplified implementation of each:
FIFO Buffer (C)
#include <stdio.h>
#define SIZE 5
int front = 0;
int rear = 0;
int buf[SIZE];
void enqueue(int item) {
if ((rear + 1) % SIZE == front) {
printf("Buffer is full\n");
return;
}
buf[rear] = item;
rear = (rear + 1) % SIZE;
}
//------------------------------------------------------------------------------
int dequeue() {
if (front == rear) {
printf("Buffer is empty\n");
return -1;
}
int item = buf[front];
front = (front + 1) % SIZE;
return item;
}
//------------------------------------------------------------------------------
int main() {
enqueue(10);
enqueue(20);
enqueue(30);
printf("Dequeued element: %d\n", dequeue());
printf("Dequeued element: %d\n", dequeue());
return 0;
}This code implements a FIFO buffer using a circular array. The enqueue function adds an item to the rear of the buffer, and the dequeue function removes an item from the front of the buffer. The front and rear pointers are used to track the buffer's beginning and end.
FILO Buffer (C)
#include <stdio.h>
#define SIZE 5
int top = -1;
int buf[SIZE];
void push(int item) {
if (top == SIZE - 1) {
printf("Buffer is full\n");
return;
}
buf[++top] = item;
}
//------------------------------------------------------------------------------
int pop() {
if (top == -1) {
printf("Buffer is empty\n");
return -1;
}
int item = buf[top];
top--;
return item;
}
//------------------------------------------------------------------------------
int main() {
push(10);
push(20);
push(30);
printf("Popped element: %d\n", pop());
printf("Popped element: %d\n", pop());
return 0;
}
This code implements a FILO buffer using an array. The push function adds an item to the top of the buffer, and the pop function removes an item from the top of the buffer. The top pointer is used to keep track of the top of the buffer.
FIFO Buffer (C++)
#include <iostream>
class FIFOBuffer {
private:
int *buffer; // Array to store the data
int capacity; // Maximum capacity of the buffer
int front; // Index of the front element
int rear; // Index of the rear element
public:
FIFOBuffer(int capacity) {
this->capacity = capacity;
buffer = new int[capacity];
front = 0;
rear = 0;
}
~FIFOBuffer() {
delete[] buffer;
}
bool isEmpty() {
return front == rear;
}
bool isFull() {
return (rear + 1) % capacity == front;
}
void enqueue(int item) {
if (isFull()) {
std::cout << "Buffer is full" << std::endl;
return;
}
buffer[rear] = item;
rear = (rear + 1) % capacity;
}
int dequeue() {
if (isEmpty()) {
std::cout << "Buffer is empty" << std::endl;
return -1;
}
int frontItem = buffer[front];
front = (front + 1) % capacity;
return frontItem;
}
};
//------------------------------------------------------------------------------
int main() {
FIFOBuffer buffer(5); // Create a FIFO buffer with capacity 5
buffer.enqueue(10); // Enqueue element 10
buffer.enqueue(20); // Enqueue element 20
buffer.enqueue(30); // Enqueue element 30
std::cout << "Dequeued element: " << buffer.dequeue() << std::endl; // Dequeue element (10)
std::cout << "Dequeued element: " << buffer.dequeue() << std::endl; // Dequeue element (20)
return 0;
}In this example, the FIFOBuffer class manages the FIFO buffer operations. The enqueue function adds new elements to the rear of the buffer, and the dequeue function removes elements from the front.
FILO Buffer (C++)
#include <iostream>
class FILOBuffer {
private:
int *buffer; // Array to store the data
int capacity; // Maximum capacity of the buffer
int top; // Index of the top element
public:
FILOBuffer(int capacity) {
this->capacity = capacity;
buffer = new int[capacity];
top = -1;
}
~FILOBuffer() {
delete[] buffer;
}
bool isEmpty() {
return top == -1;
}
bool isFull() {
return top == capacity - 1;
}
void push(int item) {
if (isFull()) {
std::cout << "Buffer is full" << std::endl;
return;
}
buffer[++top] = item;
}
int pop() {
if (isEmpty()) {
std::cout << "Buffer is empty" << std::endl;
return -1;
}
int topItem = buffer[top];
top--;
return topItem;
}
};
//------------------------------------------------------------------------------
int main() {
FILOBuffer buffer(3); // Create a FILO buffer with capacity 3 buffer.
buffer.push(10); // Push element 10
buffer.push(20); // Push element 20
buffer.push(30); // Push element 30
std::cout << "Popped element: " << buffer.pop() << std::endl; // Pop element (30)
std::cout << "Popped element: " << buffer.pop() << std::endl; // Pop element (20)
return 0;
}This code completes the FILO buffer implementation by adding elements to the stack (push) and removing elements from the stack (pop).
7.5 Data Sortings
Introduction to Data Sorting
Data sorting is a fundamental operation in computer science involving arranging data elements in a specific order, typically ascending or descending. Sorting algorithms are crucial for various applications, including data analysis, database management, and search engines.
Common Sorting Algorithms in C/C++
C offers a rich collection of sorting algorithms, each with its own strengths and weaknesses. Here are some of the most widely used sorting algorithms:
- Bubble Sort: A simple and intuitive algorithm that repeatedly compares adjacent elements and swaps them if they are in the wrong order.
- Selection Sort: An efficient algorithm that repeatedly finds the minimum element in an unsorted subarray and moves it to its correct position.
- Insertion Sort: A comparison-based algorithm that inserts elements into a sorted portion of the array, similar to building a sorted deck of cards.
- Merge Sort: A divide-and-conquer algorithm that recursively divides the array into smaller subarrays sorts them, and merges them back together.
- Quick Sort: A partition-based algorithm that recursively partitions the array around a pivot element, effectively dividing the problem into smaller subproblems.
Bubble Sort
What is Bubble Sort?
Bubble sort is a simple sorting algorithm that repeatedly compares adjacent elements and swaps them if they are in the wrong order. This process continues until the array is sorted. The algorithm is named after the way bubbles rise to the surface of a liquid, as the largest element is "bubble" up to the end of the array.
How Does Bubble Sort Work?
Bubble sort works by repeatedly iterating through the array, comparing adjacent elements, and swapping them if they are in the wrong order. This process continues until no more swaps are required, indicating that the array is sorted. In each iteration, the largest element in the unsorted portion of the array will move to its correct position, effectively reducing the unsorted portion by one element.
Implementation of Bubble Sort in C
void bubbleSort(int arr[], int size)
{
int i, j;
for (i = 0; i < size - 1; i++) {
for (j = 0; j < size - 1 - i; j++) {
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}This code defines a bubbleSort function that takes an integer array arr and its size size as parameters. The function uses nested loops to iterate through the array, comparing adjacent elements and swapping them if they are in the wrong order. The outer loop controls the number of iterations, while the inner loop compares and swaps elements within each iteration.
Example of Bubble Sort Usage
Here's an example of how to use the bubbleSort function to sort an array:
int main() {
int arr[] = {5, 2, 4, 1, 3};
int size = sizeof(arr) / sizeof(arr[0]);
bubbleSort(arr, size);
for (int i = 0; i < size; i++) {
printf("%d ", arr[i]);
}
return 0;
}This code defines an array arr with unsorted elements and calls the bubbleSort function to sort the array. It then prints the sorted array.
Time Complexity of Bubble Sort
The average and worst-case time complexity of bubble sort is $O({n^2})$, where n is the number of elements in the array. This means that the number of comparisons and swaps grows quadratically with the size of the array, making it less efficient for large datasets.
Advantages and Disadvantages of Bubble Sort
Advantages:
- Simple to understand and implement
- Efficient for small datasets
- In-place sorting algorithm
Disadvantages:
- Quadratic time complexity ($O({n^2})$) for average and worst cases
- Inefficient for large datasets
- More comparisons and swaps than other sorting algorithms
Bubble sort is a simple and intuitive sorting algorithm that is easy to understand and implement. However, its quadratic time complexity makes it less efficient for large datasets. Other sorting algorithms, such as merge sort and quick sort, offer better time complexity and performance for larger datasets.
Selection Sort
What is the Selection Sort?
Selection sort is a simple and efficient sorting algorithm that repeatedly finds the minimum element in an unsorted subarray and moves it to its correct position in the sorted portion of the array. This process continues until the entire array is sorted.
How Does Selection Sort Work?
Selection sort works by maintaining two portions of the array: a sorted portion and an unsorted portion. Initially, the sorted portion is empty, and the unsorted portion is the entire array. In each iteration, the algorithm selects the minimum element from the unsorted portion and swaps it with the element at the current index of the sorted portion. This effectively moves the minimum element to its correct position in the sorted portion.
Implementation of Selection Sort in C
Here's an example of implementing selection sort in C:
void selectionSort(int arr[], int size)
{
int minIndex;
for (int i = 0; i < size - 1; i++) {
minIndex = i;
for (int j = i + 1; j < size; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
if (minIndex != i) {
int temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
}
}This code defines a selectionSort function that takes an integer array arr and its size size as parameters. The function uses nested loops to iterate through the array, selecting the minimum element and moving it to its correct position. The outer loop controls the number of iterations, while the inner loop finds the minimum element within each iteration.
The main function creates an unsorted array, calls the selectionSort function to sort the array, and then prints the sorted array.
Example of Selection Sort Usage
The provided code demonstrates how to use the selectionSort function to sort an array:
int main() {
int arr[] = {5, 2, 4, 1, 3};
int size = sizeof(arr) / sizeof(arr[0]);
selectionSort(arr, size);
for (int i = 0; i < size; i++) {
printf("%d ", arr[i]);
}
return 0;
}This code defines an array arr with unsorted elements and calls the selectionSort function to sort the array. It then prints the sorted array.
Time Complexity of Selection Sort
The selection sort's average and worst-case time complexity is $O({n^2})$, where n is the number of elements in the array. This means that the number of comparisons and swaps grows quadratically with the size of the array, making it less efficient for large datasets.
Advantages and Disadvantages of Selection Sort
Advantages:
- Simple to understand and implement
- In-place sorting algorithm
- Stable sorting algorithm (preserves the original order of equal elements)
Disadvantages:
- Quadratic time complexity ($O({n^2})$) for average and worst cases
- Inefficient for large datasets
- More comparisons than other sorting algorithms
Selection sort is a straightforward and efficient sorting algorithm that is easy to understand and implement. However, its quadratic time complexity makes it less suitable for large datasets. Other sorting algorithms, such as merge sort and quick sort, offer better time complexity and performance for larger datasets.
Insertion Sort
What is Insertion Sort?
Insertion sort is a simple and efficient sorting algorithm that resembles the way we sort playing cards in our hands. It works by building a sorted subarray one element at a time. Initially, the sorted subarray consists of the first element, and each subsequent element is inserted into its correct position within the sorted subarray.
How Does Insertion Sort Work?
Insertion sort iterates through the array, maintaining a sorted subarray at the beginning of the array. For each unsorted element, it compares it with the elements in the sorted subarray and inserts it into its correct position. This process continues until all elements are sorted.
Implementation of Insertion Sort in C
Implementation of Insertion Sort in C
Here's an example of implementing insertion sort in C:
void insertionSort(int arr[], int size) {
for (int i = 1; i < size; i++) {
int currentElement = arr[i];
int j;
for (j = i - 1; j >= 0 && currentElement < arr[j]; j--) {
arr[j + 1] = arr[j];
}
arr[j + 1] = currentElement;
}
}This code defines an insertionSort function that takes an integer array arr and its size size as parameters. The function uses an outer loop to iterate through the unsorted elements and an inner loop to compare and insert each element into its correct position.
Example of Insertion Sort Usage
Here's an example of how to use the insertionSort function to sort an array:
int main() {
int arr[] = {5, 2, 4, 1, 3};
int size = sizeof(arr) / sizeof(arr[0]);
insertionSort(arr, size);
for (int i = 0; i < size; i++) {
printf("%d ", arr[i]);
}
return 0;
}This code defines an array arr with unsorted elements and calls the insertionSort function to sort the array. It then prints the sorted array.
Time Complexity of Insertion Sort
The average and best-case time complexity of insertion sort is $O({n^2})$, where n is the number of elements in the array. The worst-case time complexity occurs when the array is already sorted in reverse order, in which case the inner loop performs n comparisons for each iteration.
Advantages and Disadvantages of Insertion Sort
Advantages:
- Simple to understand and implement
- In-place sorting algorithm
- Stable sorting algorithm (preserves the original order of equal elements)
- Efficient for small to medium-sized datasets
Disadvantages:
- Quadratic time complexity ($O({n^2})$) for average and worst cases
- Inefficient for large datasets
- More comparisons than other sorting algorithms, especially for large datasets
Insertion sort is a versatile and straightforward sorting algorithm that is easy to understand and implement. While its quadratic time complexity makes it less efficient for large datasets, it performs well for smaller datasets and is often used in practice due to its simplicity and stability.
Merge Sort
What is Merge Sort?
Merge sort is a divide-and-conquer sorting algorithm that repeatedly divides an unsorted array into smaller subarrays, sorts them recursively, and merges them back together in sorted order. It is one of the most efficient sorting algorithms with an average and worst-case time complexity of $O(n\log n)$, where n is the number of elements in the array.
How Does Merge Sort Work?
Merge sort works by recursively dividing the unsorted array into halves until each subarray contains a single element. These single-element subarrays are naturally sorted. Then, the algorithm merges the sorted subarrays pairwise, combining them into larger sorted subarrays.
Implementation of Insertion Sort in C
void merge(int arr[], int left, int mid, int right)
{
int temp[right - left + 1];
int i, j, k;
i = left;
j = mid + 1;
k = 0;
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
temp[k] = arr[i];
i++;
} else {
temp[k] = arr[j];
j++;
}
k++;
}
while (i <= mid) {
temp[k] = arr[i];
i++;
k++;
}
while (j <= right) {
temp[k] = arr[j];
j++;
k++;
}
// Copy the merged array back to the original array
for (i = left; i <= right; i++) {
arr[i] = temp[i - left];
}
}
//------------------------------------------------------------------------------
void mergeSort(int arr[], int left, int right)
{
if (left < right) {
int mid = (left + right) / 2;
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
merge(arr, left, mid, right);
}
}This code defines a merge function that merges two sorted subarrays of an array into a single sorted subarray. It also defines a mergeSort function that recursively divides the array into subarrays, sorts them, and merges them back together. The main function creates an unsorted array, calls the mergeSort function to sort the array, and then prints the sorted array.
Example of Merge Sort Usage
Here's an example of how to use the mergeSort function to sort an array:
int main()
{
int arr[] = {5, 2, 4, 1, 3};
int size = sizeof(arr) / sizeof(arr[0]);
mergeSort(arr, 0, size - 1);
for (int i = 0; i < size; i++) {
printf("%d ", arr[i]);
}
return 0;
}This code defines an array arr with unsorted elements and calls the mergeSort function to sort the array. It then prints the sorted array.
Time Complexity of Merge Sort
The average and worst-case time complexity of merge sort is $O(n\log n)$, where n is the number of elements in the array. This makes merge sort one of the most efficient sorting algorithms for large datasets.
Advantages and Disadvantages of Merge Sort
Advantages:
- Efficient time complexity ($O(n\log n)$) for average and worst cases
- Stable sorting algorithm (preserves the original order of equal elements)
- Suitable for large datasets
Disadvantages:
- Recursion can cause overhead for small datasets
- Requires additional memory for temporary arrays
- More complex implementation compared to simpler algorithms
Merge sort is a powerful and efficient sorting algorithm that is well-suited for large datasets. Its divide-and-conquer approach and logarithmic time complexity make it popular for various applications.
Quick Sort
What is Quick Sort?
Quicksort is a divide-and-conquer sorting algorithm that recursively partitions an unsorted array around a pivot element, effectively dividing the problem into smaller subproblems. It is one of the most efficient sorting algorithms with an average time complexity of $O(n\log n)$, where n is the number of elements in the array.
How Does Quick Sort Work?
Quicksort works by selecting a pivot element from the array. The pivot element is then placed in its correct position in the sorted array, and the remaining elements are partitioned around it. The algorithm then recursively applies the same process to the smaller subarrays until all elements are sorted.
Implementation of Quick Sort in C
Implementation of Quick Sort in C
Here's an example of implementing quick sort in C:
void swap(int *a, int *b)
{
int temp;
temp = *a;
*a = *b;
*b = temp;
}
//------------------------------------------------------------------------------
int partition(int arr[], int low, int high)
{
int pivot = arr[high];
int i = (low - 1);
for (int j = low; j < high; j++) {
if (arr[j] <= pivot) {
i++;
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]);
return (i + 1);
}
//------------------------------------------------------------------------------
void quickSort(int arr[], int low, int high)
{
if (low < high) {
int pi = partition(arr, low, high);
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}This code defines a partition function that partitions the array around a pivot element and returns the index of the pivot element in its correct position. It also defines a quickSort function that recursively partitions and sorts the array. The main function creates an unsorted array, calls the quickSort function to sort the array, and then prints the sorted array.
Example of Quick Sort Usage
Here's an example of how to use the quickSort function to sort an array:
int main()
{
int arr[] = {5, 2, 4, 1, 3};
int size = sizeof(arr) / sizeof(arr[0]);
quickSort(arr, 0, size - 1);
for (int i = 0; i < size; i++) {
printf("%d ", arr[i]);
}
return 0;
}
This code defines an array arr with unsorted elements and calls the quickSort function to sort the array. It then prints the sorted array.
Time Complexity of Quick Sort
The average time complexity of quicksort is $O(n\log n)$, where n is the number of elements in the array. However, the worst-case time complexity is $O({n^2})$, which occurs when the pivot element is always the smallest or largest element in the array.
Advantages and Disadvantages of Quick Sort
Advantages:
- Efficient average time complexity ($O(n\log n)$)
- Suitable for large datasets
- In-place sorting algorithm
Disadvantages:
- The worst-case time complexity of $O({n^2})$
- Performance depends on the choice of pivot element
- More complex implementation compared to simpler algorithms
Quicksort is a powerful and efficient sorting algorithm that is well-suited for large datasets. Its average time complexity of $O(n\log n)$ makes it a popular choice for various applications. However, it is important to note that its performance can be affected by the choice of pivot element. If carefully chosen, the pivot element can significantly improve the performance of quicksort. However, if consistently chosen poorly, the algorithm can degrade to $O({n^2})$ time complexity, which is less efficient than other sorting algorithms like merge sort.
Quicksort is a versatile and efficient sorting algorithm that balances speed and simplicity. It is a valuable tool for data scientists and programmers who need to sort large datasets.
Advantages of Arrays
Arrays offer several advantages, including:
- Efficient data storage: They provide a compact way to store a collection of related data.
- Organized data access: Elements are organized and can be accessed using indices.
- Random access: Any element can be directly accessed in constant time.
- Cache locality: Elements stored in contiguous memory locations, improving memory access speed.
Applications of Arrays
Arrays are widely used in various applications, such as:
- Data representation: Storing numerical data, characters, strings, and objects.
- Image processing: Manipulating and analyzing digital images.
- Scientific computing: Performing mathematical calculations and simulations.
- Algorithm implementation: Implementing various algorithms, such as sorting, searching, and data structures.
In summary, arrays are fundamental building blocks in C/C++ programming, providing an efficient and organized way to manage data collections. Their versatility and wide range of applications make them essential tools for programmers.