Lesson 04: Simplification of Boolean Expressions
4.1 Boolean Algebra
Simplifying Boolean expressions using Boolean algebra is a fundamental skill in digital logic design, allowing for the optimization of logic circuits by reducing the number of gates and connections required. This process involves applying a set of rules and theorems to manipulate and minimize Boolean expressions without changing their logical functionality.
Basic Rules of Boolean Algebra
Tips for Simplifying Boolean Expressions
- Identify Opportunities: Look for opportunities to apply simplification laws, especially the Idempotent, Inverse, and De Morgan's Laws.
- Combine Like Terms: Use the Distributive Law to factor out common terms and reduce the expression.
- Eliminate Redundancies: Apply the Idempotent Law to eliminate redundant terms.
- Check for Complements: Use Inverse Laws and De Morgan's Theorems to simplify terms involving variable complements.
4.2 Karnaugh Maps (K-Maps)
Karnaugh map (K-map) is a graphical tool that is used to simplify Boolean expressions and minimize logic circuits. They offer a visual representation of minterms and prime implicants, making it easier to identify redundancies and optimize logic functions. K-maps are especially useful for functions with three or four variables but can also be applied to larger functions with careful manipulation.
Constructing Karnaugh Maps
- Draw the Grid: The number of rows and columns in a K-map is determined by the number of variables.
- For 2 variables, there's a 2x2 K-map (4 cells).
- For 3 variables, there's a 4x2 or 2x4 K-map (8 cells).
- For 4 variables, there's a 4x4 K-map (16 cells).
- Label the Grid: Label the rows and columns with Gray code (a sequence of binary numbers where only one bit changes at a time) to represent all possible combinations of the input variables.
- Fill the Grid: Fill the K-map cells with 1s and 0s based on the function's truth table.
- 1s represent minterms where the function outputs 1 (true).
- 0s represent minterms where the function outputs 0 (false).
Two Variables K-Map
F(x, y)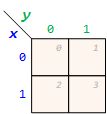
Three variables K-Map
F(x, y, z)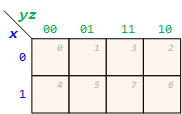
Four Variables K-Map
F(w, x, y, z)
Simplifying Boolean Functions with K-Maps
- Identify Groups:
- Look for adjacent groups of 1s (for SOP form) or 0s (for POS form) in the map. Make each rectangle groups as large as possible and must contain a number of cells that have a power of 2 (e.g., 1, 2, 4, 8, ...) to minimize the number of literals in each term.
- Make as few rectangle groups as possible to minimize the number of terms in the final expression.
- Form Groups: Groups can wrap around the edges of the map. The aim is to cover all the 1s (or 0s) in the map with the minimum number of groups.
- Write the Simplified Expression: For each group, determine the common variables (the variables that don't change within the group). Write these variables as a product term for SOP (or sum term for POS). The simplified function is the sum of these product terms (or the product of these sum terms).
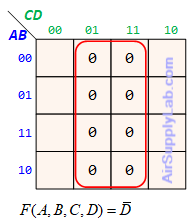
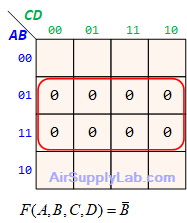
Example of K-maps with 4 variables for SoP Forms
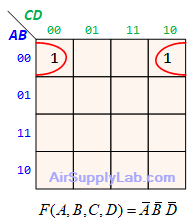
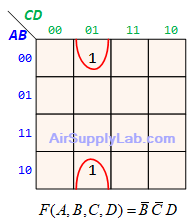
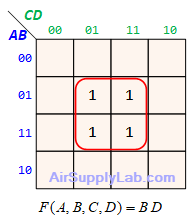
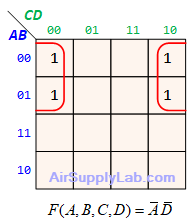
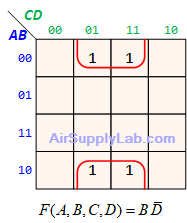
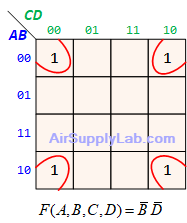
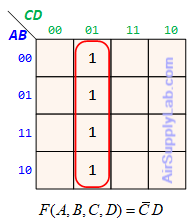
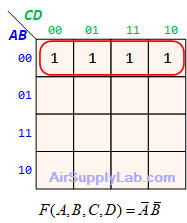
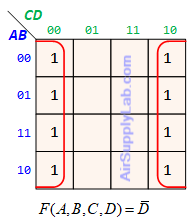
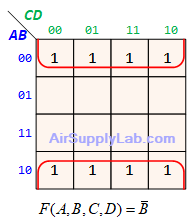
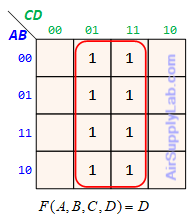
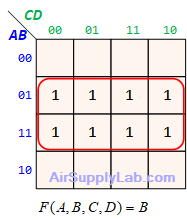
Example of K-maps with 4 variables for PoS Forms
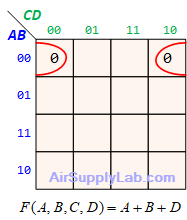
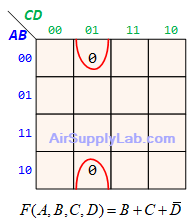
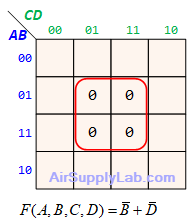
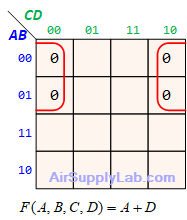
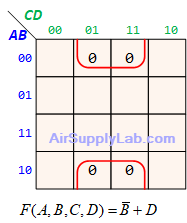
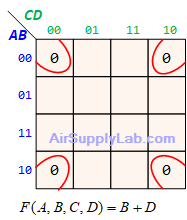
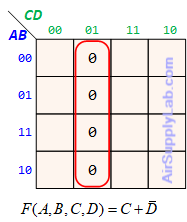
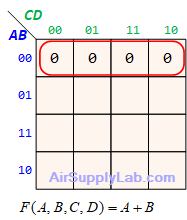
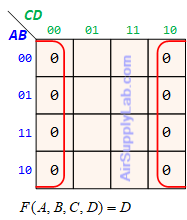
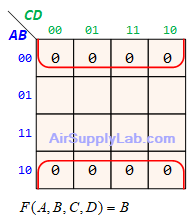
Don't Care (Logic X)
In digital logic, Karnaugh Maps (K-Maps) help simplify Boolean expressions. "Don't care" conditions add another layer of flexibility, allowing for further minimization when used strategically. Here's a detailed breakdown:
What are "don't cares"?
- These are input combinations for which the output value doesn't matter.
- "Don't care" conditions occur when the value of a cell in a truth table is irrelevant to the circuit's behavior.
Representing "don't cares" in K-Maps
- In K-Maps, "don't care" cells are typically denoted by an 'X' instead of "0" or "1".
Handling "Don't Care" Conditions in K-Maps
- You can treat a "don't care" as either "0" or "1" when grouping adjacent cells in the K-Map.
- This flexibility allows the forming of larger groups, leading to a simpler, minimized expression.
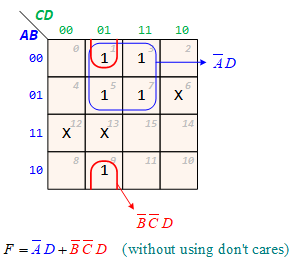
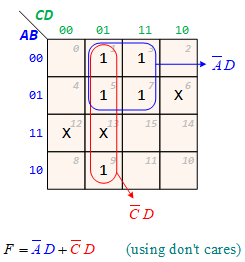
Example: With Don't Cares
- F(A, B, C, D) = Σ m(1, 3, 5, 7, 9) + d(6, 12, 13)
4.3 Tabulation Method
Tabulation Method
The Tabulation Method, also known as the Quine-McCluskey algorithm, is a systematic approach for simplifying Boolean algebra expressions in Digital Logic Design. It is particularly useful for minimizing complex Boolean functions to their simplest form, making it easier to design efficient digital circuits. This method is especially effective for functions with many variables, where Karnaugh maps (K-maps) become cumbersome.
Steps to Apply the Tabulation Method:
- List the Minterms: Start by listing all the minterms (combinations of variables that yield a true result) of the function in binary form.
- Group the Minterms: Group the minterms based on the number of 1s they contain. This is because minterms with a similar number of 1s can potentially be combined.
- Combine Minterms: Compare minterms within adjacent groups. If two minterms differ by only one bit, they can be combined into a term with a dash (-) in the differing position, indicating that the particular bit can be either 0 or 1. This process of combination reduces the complexity of the expression.
- Repeat the Combination Step: Continue combining terms until no further combinations are possible. The resulting terms are known as prime implicants.
- Identify Essential Prime Implicants: Determine which prime implicants are essential. An essential prime implicant covers a minterm that no other prime implicant covers.
- Construct the Prime Implicant Chart: If there are non-essential prime implicants, construct a chart with prime implicants on one axis and the minterms they cover on the other. This helps in selecting the minimum number of prime implicants needed to cover all minterms.
- Select the Minimum Cover: Choose a set of prime implicants that covers all the minterms of the function with the smallest number of terms.
Example: Simplifying a Boolean Function
Consider a Boolean function F(w, x, y,z) = Σ m(0, 2, 5, 7, 10, 13, 14, 15)
Step1: List the Minterms in Binary Form
- m0 = 0000
- m2 = 0010
- m5 = 0101
- m7 = 0111
- m10 = 1010
- m13 = 1101
- m14 = 1110
- m15 = 1111
Step2: Group by Number of 1s
- Group 0: 0000
- Group 1: 0010
- Group 2: 0101, 1010
- Group 3: 0111, 1101, 1110
- Group 4: 1111
Step 3: Combine Minterms and Identify Prime Implicants
- Combine 0000 and 0010 to 00-0
- Combine 0010 and 1010 to -010
- Combine 0101 and 0111 to 01-1
- Combine 0101 and 1101 to -101
- Combine 1010 and 1110 to 1-10
- Combine 0111 and 1111 to -111
- Combine 1101 and 1111 to 11-1
- Combine 1110 and 1111 to 111-
Step 4: Continue to Combine Minterms and Identify Prime Implicants
- Combine 01-1 and 11-1 to -1-1
- Combine -101 and -111 to -1-1
- No further combinations are possible, so we have prime applicants: 00-0, -010, -1-1, 1-10, and 111-
Step 5: Identify Essential Prime Implicants
- For this example, assume all are essential for simplicity.
Step 6 & 7: Select the Minimum Cover
- Since all prime implicants are considered essential, our minimal expression includes them all:
Fmin(w, x, y, z) = w x z + x y z + x z + w y z + w x y
Using the Tabulation Method, this example simplifies the Boolean function to its minimal form. In practice, the prime implicant chart in Step 6 is crucial for identifying essential prime implicants when dealing with non-trivial functions, ensuring the most efficient combination of terms for the minimal expression.

Benefits of the Tabulation Method:
- A systematic approach for identifying prime implicants.
- Offers various minimization techniques to find optimal solutions.
- Applicable to functions with a large number of variables.
Questions
- When a Karnaugh map has four rows or columns, they are numbered 00, 01, 11, 10 instead of 00, 01, 10, 11. Why?
- Simplify the following Boolean functions using three-variable K-maps:
- $F(x,y,z) = x\,y + \overline x \,\overline y \,\overline z + \overline x \,y\,\overline z $
- $F(x,y,z) = \overline x \,\overline y + y\,z + \overline x \,y\,\overline z $
- $F(x,y,z) = \overline x \,y + y\,\overline z + \overline y \,\overline z $
- Simplify the following Boolean functions:
- F(x, y, z) = Σ m(0, 1, 5, 7)
- F(x, y, z) = Σ m(1, 2, 3, 6, 7)
- F(w, x, y, z) = Σ m(1, 3, 7, 11, 15) + d(0, 2, 5)
- F(w, x, y, z) = Σ m(4, 5, 6, 7, 12) + d(0, 8, 13)
- F(w, x, y, z) = Σ m(1, 6, 10, 11, 12, 13, 15) + d(4, 5, 7, 8, 14)
- Simplify the following Boolean functions:
- F(A, B, C, D) = ∏ M(1, 3, 5, 7, 13, 15)
- F(A, B, C, D) = ∏ M(1, 3, 6, 9, 11, 12, 14)
- Simplify the following expression to (1) SoP and (2) PoS:
- $\overline A \,\overline C + \overline B \,\overline C + B\,\overline C + A\,B$
- $(\overline A + B + \overline D ) \cdot (\overline A + \overline B + \overline C ) \cdot (\overline A + \overline B + C) \cdot (\overline B + C + \overline D )$
- Implement the following Boolean expression with XOR and AND gates:
$$F = A\,\overline B \,C\,\overline D + \overline A \,B\,C\,\overline D + A\,\overline B \,\overline C \,D + \overline A \,B\,\overline C \,D$$